Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 4.1 - Ex. 17
Esboce o gráfico de à mão e use seu esboço para encontrar os valores máximos e mínimos locais e absolutos de .
Passo 1
Eaee, belezinha?? Bom... o enunciado nos dá a seguinte função com seu intervalo:
Queremos esboçar a função mostrada e, em seguida, mostrar os valores de mínimos e máximos locais e absolutos da função.
Bom... Mínimos locais são os pontos onde a função alcança seu valor mais baixo em uma vizinhança, enquanto máximos locais são os pontos onde a função alcança seu valor mais alto. Podemos pensar neles como pontos críticos onde a inclinação da função é zero. Assim:
Já quando falamos de mínimos e máximos absolutos são os valores mais baixos e mais altos da função em todo o seu domínio, isso inclui a comparação entre os pontos locais e também entre os extremos do intervalo dado.
Agora bora lá!! 😉
Passo 2
O gráfico trata-se de uma função do segundo grau com concavidade voltada para cima e centrada na origem.
Assim, aplicando o intervalo, temos o seguinte esboço:
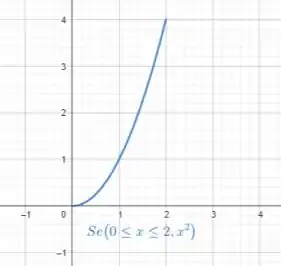
Passo 3
Pelo gráfico, podemos ver que temos não houve nenhum pico ou vale na função dentro do intervalo definido.
Assim, podemos dizer que
- Maximo local: Nenhum
- Mínimo local: Nenhum
- Máximo absoluto: Nenhum
- Mínimo absoluto: Nenhum
E como nosso intervalo é aberto nos extremos
Note que os pontos não são levados em conta pois o intervalo é aberto em e em
Resposta
Não há nenhum ponto de máximo ou mínimo locais e absolutos