Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 4.1 - Ex. 16
Esboce o gráfico de à mão e use seu esboço para encontrar os valores máximos e mínimos locais e absolutos de .
Passo 1
Oieeee galerinha do RA, bora macetar essa comigo?
Para esboçar o gráfico da função
E encontrar os valores máximos e mínimos locais e absolutos, siga os passos abaixo:
Vamos analisar a Função
A função é uma função linear. Uma função linear não possui máximos ou mínimos locais, mas podemos identificar o valor máximo ou mínimo absoluto dependendo do intervalo fornecido.
Calcular os Valores nos Pontos Críticos do Intervalo
Os pontos críticos do intervalo dado são (o extremo direito do intervalo) e o comportamento para
Passo 2
Para :
Para :
Quando , a função tende para
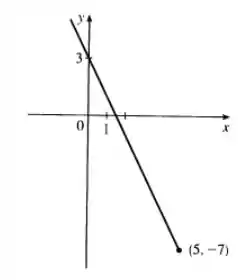
Esboçar o Gráfico
Para esboçar o gráfico de
1. Identifique o ponto no gráfico.
2. Desenhe uma linha que passa por e continua para a esquerda, subindo linearmente, pois a função é decrescente (a inclinação é ).
Passo 3
Para determinar Máximos e Mínimos
- Máximo absoluto: O valor máximo absoluto ocorre quando .
Então, não há um valor específico, mas sabemos que a função tende para
- Mínimo absoluto: O valor mínimo absoluto ocorre em
Esboço do Gráfico
Para desenhar o gráfico à mão:
1. Plote o ponto
2. Trace uma linha reta passando por que continua subindo para a esquerda conforme diminui, sem limite superior.
Passo 4
Resumo dos Valores Máximos e Mínimos
- Máximo absoluto: Não há valor específico porque quando
- Mínimo absoluto: em .
Não existem máximos ou mínimos locais adicionais, pois a função é linear e monotônica decrescente dentro do intervalo especificado.
Resposta
Vide o passo a passo.