Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.3 - Ex. 15
Encontre a equação cartesiana para a curva descrita pela equação polar dada.
Passo 1
Oii, tudo certinho contigo?? Vamos resolver uma questãozinha legal???
Bom... Queremos encontrar a equação cartesiana (ou seja, uma ) para a curva descrita pela seguinte equação polar:
Para isso, a gente precisa saber que podemos relacionar as coordenadas cartesianas com as coordenadas polares da seguinte forma:
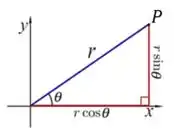
Veja que o ponto pode ser dado tanto em coordenadas cartesianas como em coordenadas polares.
Veja também que temos um triângulo retângulo. Assim, podemos fazer algumas relações!! 😉
Passo 2
Perceba que o triângulo tem hipotenusa e catetos e . Assim, pelo Teorema de Pitágoras, temos:
O enunciado nos disse que:
Então jogando isso ali, a gente fica com:
Que é a equação cartesiana de um círculo de raio . 😉