Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.3 - Ex. 5
As coordenadas cartesianas de um ponto são dadas.
- Encontre as coordenadas polares do ponto, onde e .
- Encontre as coordenadas polares do ponto, onde e .
Passo 1
Olá, meu amigo. Vou te ajudar a resolver essa atividade.
Aqui, nós iremos, eu e você, encontrarmos as coordenadas polares dos pontos:
Para isso, iremos utilizar a relação:
A figura abaixo vai te ajudar a visualizar melhor como é a relação entre coordenadas polares e coordenadas cartesianas:
Passo 2
- Vamos lá a gente vai usar as relações:
- Vamos seguir o mesmo raciocínio!
Então a gente tem:
É o nosso ponto. Sendo assim o :
Aí o ângulo, a gente precisa encontrar tanto para quanto para .
Esse círculo trigonométrico vai salvar sua vida agora:
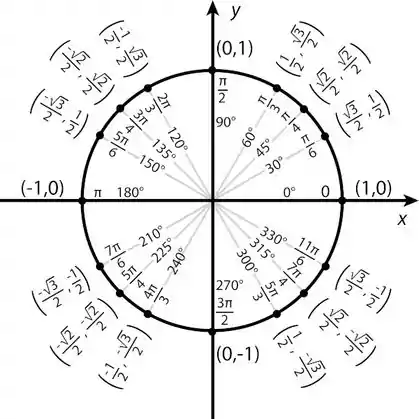
Ou seja, o ângulo então é:
Isso pro raio positivo!
O ponto é
Pro raio negativo, vamos ter:
Aí o ângulo fica sendo o
E o ponto: .
Passo 3
O ponto agora é:
Beleza, pro raio positivo:
Com o nosso círculo:
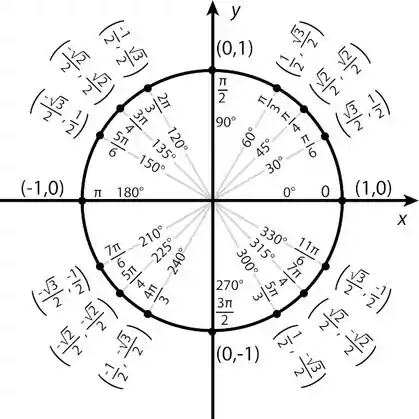
Aqui o ângulo então é certo?
O ponto então é:
Agora a gente faz com negativo:
Aqui então o ângulo tá no quarto quadrante, é o
Aí o ponto é: