Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 10.3 - Ex. 15

Encontre a equação cartesiana para a curva descrita pela equação polar dada.

15. r = 2

Passo 1

Queremos encontrar uma equação cartesiana para a curva com equação r = 2 .

Para isso, a gente tem que saber da relação entre coordenas cartesianas e polares.

Essa relação a gente pode notar aqui:

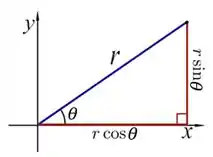
Onde temos que:

x = r cos ⁡ θ

y = r   s e n   θ

Agora bora aplicar!! 😉

Passo 2

Note que uma coordenada cartesiana trabalha com o seno e outra com o cosseno.

Hm... sabe de alguma relação trigonométrica que envolva esses dois??

Siiim!! A gente sabe que sin 2 ⁡ ϕ + cos 2 ⁡ ϕ = 1 .

Então vamos fazer x 2 + y 2 :

x 2 + y 2 = r 2 cos 2 ⁡ θ + r 2 s e n 2 θ

Colocando o r 2 em evidência:

x 2 + y 2 = r 2 ( cos 2 ⁡ θ + s e n 2 θ )

Fa relação trigonométrica que acabamos de apresentar, podemos fazer:

x 2 + y 2 = r 2 ( 1 )

Mas o enunciado nos disse que r = 2 , portanto:

x 2 + y 2 = 4  

Então essa é a equação cartesiana que estávamos procurando, e ela representa um círculo de raio r = 2 centrada na origem.

Resposta

x 2 + y 2 = 4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Plote o ponto cujas coordenadas cilíndricas são dadas. Depois, determine as coordenadas retangulares do ponto. 3 , 0 , - 6
Plote o ponto cujas coordenadas cilíndricas são dadas. Depois, determine as coordenadas retangulares do ponto. 1 , π , e
Plote o ponto cujas coordenadas cilíndricas são dadas. Depois, determine as coordenadas retangulares do ponto. 1 , 3 ⋅ π 2 , 2
Converta de coordenadas retangulares para coordenadas cilíndricas 1 , - 1,4
Plote o ponto cujas coordenadas esféricas são dadas. Depois, determine as coordenadas retangulares do ponto. 1 , π 6 , π 6