Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 10.3 - Ex. 17

Encontre a equação cartesiana para a curva descrita pela equação polar dada.

r = 2 cos ⁡ θ

Passo 1

Queremos encontrar uma equação cartesiana para a curva com equação r = 2 cos ⁡ θ .

Para isso, a gente tem que saber da relação entre coordenas cartesianas e polares.

Essa relação a gente pode notar aqui:

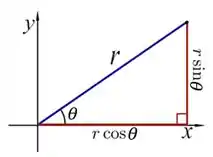
Onde temos que:

x = r cos ⁡ θ

y = r   s e n   θ

r 2 = x 2 + y 2

Agora bora aplicar!! 😉

Passo 2

Multiplicando os dois lados da equação r = 2 cos ⁡ θ   por r , temos que:

r 2 = 2 r cos ⁡ θ

Então substituindo r 2 pela relação que vimos no passo 1, temos:

x 2 + y 2 = 2 x

Colocando tudo para o lado esquerdo, temos:

x 2 - 2 x + y 2 = 0

Somando + 1 dos dois lados ficamos com:

x 2 - 2 x + 1 + y 2 = 1

Pelos produtos notáveis, sabemos que x 2 - 2 x + 1 = x - 1 2 , logo:

x - 1 2 + y 2 = 1

Então, temos um circulo de raio 1 centrado em ( 1,0 ) .

Resposta

x - 1 2 + y 2 = 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Substitua as equações polares nos Exercícios 27-52 por equações cartesianas equivalentes. Em seguida, descreva ou identifique o gráfico. r = 8 sen ⁡ θ
Substitua as equações cartesianas nos Exercícios 53-66 por equações polares equivalentes. y = 1
Substitua as equações polares nos Exercícios 27-52 por equações cartesianas equivalentes. Em seguida, descreva ou identifique o gráfico. r sen ⁡ 2 π 3 - θ = 5
Substitua as equações cartesianas nos Exercícios 53-66 por equações polares equivalentes. x - 5 2 + y 2 = 25
Substitua as equações polares nos Exercícios 27-52 por equações cartesianas equivalentes. Em seguida, descreva ou identifique o gráfico. r = 3 cos ⁡ θ