Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.5 - Ex. 36
Encontre uma equação para a cônica que satisfaz as condições dadas
36. Parábola, eixo vertical, passando por
Passo 1
Olá, meu amigo. Vou te ajudar a resolver essa atividade.
Nessa questão, nos foi dado o nome da cônica, seu eixo e três pontos pelo qual ela passa, para encontrarmos sua equação.
Bom, sabemos que é uma parábola, e parábolas tem equações no formato:
ou
A gente pode ver abaixo os gráficos genérico das parábolas centradas em
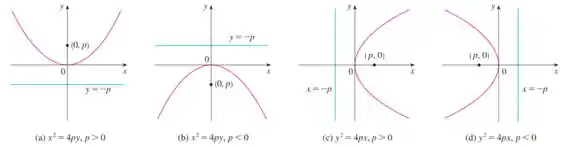
como essa é uma parábola no eixo vertical, tem o formato:
Bom, como temos três pontos pelos quais ela passa, podemos fazer um sistema:
E assim encontrarmos o e o ponto .
Passo 2
De ficamos com:
De temos:
Substituindo isso na primeira equação que encontramos, ficamos com:
Vamos trocar na segunda equação para ver o que achamos:
Agora que temos o valor de e podemos substituí-los na equação :
Show! Já temos o valor de e , para nossa equação ficar completa falta apenas acharmos . Para isso basta voltar na equação de e trocar os valores que já temos:
Juntando tudo isso, nossa equação da forma fica sendo: