Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 11.Exercícios adicionais e avançados - Ex. 17

  1. Encontre uma equação em coordenadas polares para a curva:

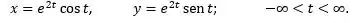
  2. Encontre o comprimento da curva de t = 0 a t = 2 π .

Passo 1

Oi galerinha! Para resolvermos o item a. deste exercício, precisamos relembrar as equações que que relacionam as coordenadas polares e cartesianas:

E do enunciado temos:

Podemos considerar que t = θ , logo:

x = e 2 θ cos ⁡ θ y = e 2 θ sen ⁡ θ

Então, a nossa coordenada polar será:

r = e 2 θ

Passo 2

Já no item b., queremos encontrar o comprimento da curva, para quando 0 < t < 2 π . Se uma curva C é definida parametricamente por x = f t e y = g t , a ≤ t ≤ b , em que f ' e g ' são contínuas e não simultaneamente zero em a ,   b , e C é percorrida exatamente uma vez conforme t aumenta de t = a para t = b , então o comprimento de C é a integral definida:

L = ∫ a b d x d t 2 + d y d t 2 d t

Então primeiramente iremos calcular as derivadas de x e y , onde:

E as derivadas para exponencial, cosseno e seno são:

y = e u → y ' = u ' ∙ e u                           y = cos ⁡ u → y ' = - u ' ∙ sen ⁡ u y = sen ⁡ u → y ' = u ' ∙ cos ⁡ u      

E para calcular ambas as derivadas, precisaremos utilizar a Regra do Produto, onde:

y = u ∙ v → y ' = u ' ∙ v + u ∙ v '

  • Para x = e 2 t cos ⁡ t :

    • u = e 2 t → u ' = 2 ∙ e 2 t         v = cos ⁡ t → v ' = - sen ⁡ t

    Substituindo na equação da Regra do Produto:

    x ' = d x d t = 2 ∙ e 2 t ∙ cos ⁡ t + e 2 t ∙ - sen ⁡ t

    d x d t = 2 ∙ e 2 t ∙ cos ⁡ t - e 2 t ∙ sen ⁡ t

    d x d t = e 2 t 2 cos ⁡ t - sen ⁡ t

  • Agora faremos o mesmo para y = e 2 t sen ⁡ t :

u = e 2 t → u ' = 2 ∙ e 2 t v = sen ⁡ t → v ' = cos ⁡ t

Substituindo na equação da Regra do Produto:

y ' = d y d t = 2 ∙ e 2 t ∙ sen ⁡ t + e 2 t ∙ cos ⁡ t

d y d t = e 2 t 2 sen ⁡ t + cos ⁡ t

Passo 3

Então temos:

d x d t 2 + d y d t 2 = e 2 t 2 cos ⁡ t - sen ⁡ t 2 + e 2 t 2 sen ⁡ t + cos ⁡ t 2

= e 4 t 2 cos ⁡ t - sen ⁡ t 2 + e 4 t 2 sen ⁡ t + cos ⁡ t 2

Expandido a equação

= e 4 t 4 cos 2 ⁡ t - 4 cos ⁡ t sen ⁡ t + sen 2 ⁡ t + 4 sen 2 ⁡ t + 4 cos ⁡ t sen ⁡ t + cos 2 ⁡ t

= e 4 t 4 cos 2 ⁡ t + 4 sen 2 ⁡ t + cos 2 ⁡ t + sen 2 ⁡ t - 4 cos ⁡ t sen ⁡ t + 4 cos ⁡ t sen ⁡ t

= e 4 t 4 cos 2 ⁡ t + sen 2 ⁡ t + cos 2 ⁡ t + sen 2 ⁡ t - 4 cos ⁡ t sen ⁡ t + 4 cos ⁡ t sen ⁡ t

Sabemos que:

cos 2 ⁡ t + sen 2 ⁡ t = 1

Logo:

d x d t 2 + d y d t 2 = e 4 t 4 + 1

d x d t 2 + d y d t 2 = 5 ∙ e 4 t

Passo 4

Então a integral fica da seguinte forma:

L = ∫ 0 2 π 5 ∙ e 4 t d t = 5 ∙ ∫ 0 2 π e 4 t d t

Considerando:

u = 4 t

Logo:

d u = 4 d t → d t = d u 4

= 5 ∙ ∫ e u   d u 4

= 5 4 ∙ ∫ e u   d u

= 5 4 ∙ ∫ e u 1 2   d u = 5 4 ∙ ∫ e u 2   d u

Onde:

v = u 2

Logo:

d v = d u 2 → d u = 2 ∙ d v

= 5 4 ∙ ∫ e v ∙   2 ∙ d v = 5 2 ∙ e v

Substituindo os valores, para voltarmos para o inicial:

L = 5 2 ∙ e 4 t 0 2 π

= 5 2 ∙ e 4 ∙ 2 π - e 4 ∙ 0

= 5 2 ∙ e 8 π - e 0

= 5 2 ∙ e 4 π - 1

Resposta

  1. r = e 2 θ ;
  2. L = 5 2 ∙ e 4 π - 1 .

Exercícios de Livros Relacionados

Substitua as equações polares nos Exercícios 27-52 por equações cartesianas equivalentes. Em seguida, descreva ou identifique o gráfico.29. rs e nθ = 0
Substitua as equações polares nos Exercícios 27-52 por equações cartesianas equivalentes. Em seguida, descreva ou identifique o gráfico.44. c o s 2 θ = s e n 2 θ
Substitua as equações polares nos Exercícios 27-52 por equações cartesianas equivalentes. Em seguida, descreva ou identifique o gráfico.40. r = 4t gθs e cθ
Substitua as equações polares nos Exercícios 27-52 por equações cartesianas equivalentes. Em seguida, descreva ou identifique o gráfico.35. r2 = 1
Substitua as equações polares nos Exercícios 27-52 por equações cartesianas equivalentes. Em seguida, descreva ou identifique o gráfico.45. r 2 = - 4 rc o s θ