Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.1 - Ex. 63
Uma caixa sem tampa será feita com um pedaço retangular de papelão com dimensões de polegadas, cortando-se quadrados iguais de lado em cada canto e, depois, dobrando-se as laterais para cima, conforme mostra a figura. Expresse o volume da caixa em função de .
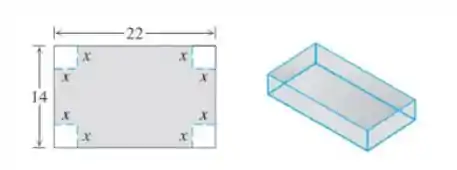
Passo 1
A questão pede que escrevamos o volume da caixa em função das dimensões do quadrado recortado. Para isto, precisamos determinar cada uma das 3 dimensões da caixa, visto que o seu volume é calculado através da seguinte equação:
Ao escrevermos cada um desses comprimentos como uma função de e multiplicarmos todos eles, obteremos o volume da nossa caixa em função de . Por fim, determinaremos o domínio da nossa função
Passo 2
A altura da caixa será exatamente o comprimento do recorte. Logo:
Passo 3
O comprimento do pedaço retangular é igual a . Ao fazer um recorte no valor de ( para cada lado), teremos o comprimento da nossa caixa. Isto é:
Passo 4
A largura do pedaço retangular é igual a . Ao fazer um recorte no valor de ( para cada lado), teremos a largura da nossa caixa. Isto é:
Passo 5
O volume da nossa caixa é obtido multiplicando cada uma das medidas obtidas nos passos anteriores. Sendo assim, temos:
Passo 6
Ao realizar o recorte do pedaço retângulo, é necessário que sobre um pedaço de papelão em cada um dos lados para que ele possa formar as laterais da caixa. Sendo assim, temos duas restrições para o nosso problema, tanto em relação do comprimento quanto da largura:
Neste problema, predomina-se a restrição da largura , pois valores não é possível cortar quadrados de lado maior que 7, visto que não há largura suficiente.