Enunciado
Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 2.17 - Ex. 3
- Construir os gráficos das funções polinomiais . Dar o domínio e conjunto imagem.
)
Passo 1
Inicialmente vamos determinar apenas o domínio a imagem tiraremos pelo gráfico, é a forma mais fácil de se determinar a imagem!
O Domínio de uma função polinomial é sempre o conjunto dos Reais.
Para funções polinomiais, jogaremos valores aleatórios e ligaremos os pontos, já que não temos conhecimento o bastante para desenhar esses gráficos!
Passo 2
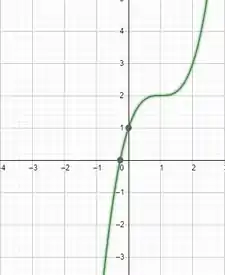
Para a primeira função faremos uma tabela de valores de a , dessa forma:
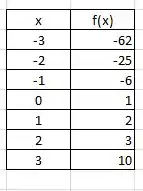
Assim poderíamos ter o esboço do gráfico e ficaria mais ou menos assim:
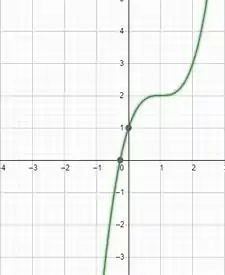
Do gráfico, podemos tirar a imagem também!!! Verificando quais os valores que o gráfico consegue alcançar! Todos os valores em o gráfico consegue chegar!
Isso quer dizer que a imagem dessa função são os Reais!
Para a função , faremos o mesmo procedimento:
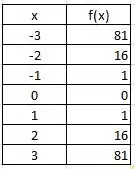
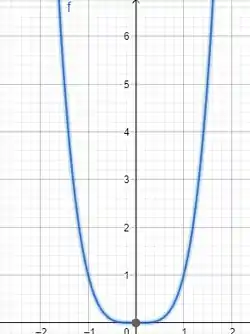
O gráfico agora ficaria mais ou menos assim.
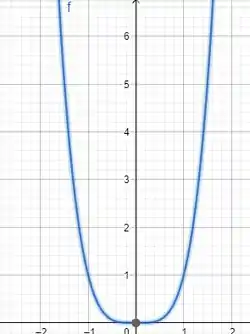
Se seguirmos o gráfico, vamos ver que a imagem dele é apenas os valores positivos, ele nunca “alcança” valores negativos!
Passo 3
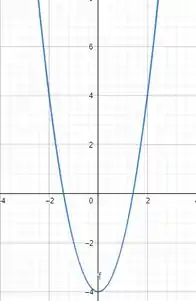
A última é uma função quadrática, então usaremos as propriedades de uma função quadrática!
Concavidade para cima, já que para , temos que:
E vamos calcular as raízes:
Temos duas raízes diferentes.
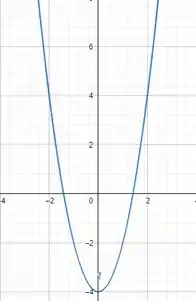
A imagem dessa função são todos os valores acima de , vai de até o .
Resposta
a)
b)
c)
