Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.3 - Ex. 21
Encontre uma equação polar para a curva representada pela equação cartesiana dada.
Passo 1
Eaee, belezinha?? Bom... o enunciado nos deu a seguinte equação cartesiana:
Queremos transformar ela em uma equação polar.
Sabemos que da coordenada cartesiana para a coordenada polar fazemos que:
E
Mas de onde saíram essas fórmulas e essas variáveis???
Bom... um ponto pode ser dado tanto em coordenadas quanto em coordenadas polares , veja:
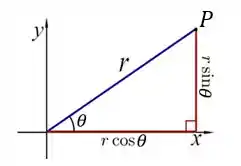
Agora bora aplicar!! 😉
Passo 2
Note, que só precisamos, neste caso, da coordenada , e sabemos que também é igual a , assim:
Como queremos agora, em coordenada polar, usaremos apenas igualdade:
Isolando o , ficamos com:
Note que . Então, temos que:
Resposta
Exercícios de Livros Relacionados
Esboce as retas nos Exercícios 23-28. Determine também uma equação cartesiana para cada reta. r = - 3 2 cos sec θ
Encontre equações polares para os círculos nos Exercícios 33-36. Esboce cada círculo no plano coordenado e rotule-o com suas equações cartesianas e polares. x 2 + y 2 - 3 x = 0
Encontre equações polares para os círculos nos Exercícios 33-36. Esboce cada círculo no plano coordenado e rotule-o com suas equações cartesianas e polares. x 2 + y 2 - 2 y = 0
Esboce as retas nos Exercícios 23-28. Determine também uma equação cartesiana para cada reta. r = 2 sec θ
Esboce as retas nos Exercícios 23-28. Determine também uma equação cartesiana para cada reta. r c o s θ + π 3 = 2 3