Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 3.1 - Ex. 61
61. Encontre uma equação para a reta normal á curva que seja paralela à reta .
Passo 1
Oiii, vamos fazer essa questão! Queremos achar a equação para a reta normal a curva:
Mas o que que é uma reta normal?!
É uma reta perpendicular à reta tangente a curva neste ponto!
Para uma reta ser perpendicular à outra os seus coeficientes angulares tem que ser inversos, ou seja:
Além disso o enunciado diz que essa reta normal é paralela à:
Retas paralelas tem o mesmo coeficiente angular! Que nesse caso é igual a:
Esse vai ser o coeficiente angular da reta normal a curva, . Agora podemos achar o coeficiente angular da reta tangente:
Passo 2
Show! Agora precisamos achar um ponto que pertença a reta normal. Ele pode ser o ponto de intersecção da reta tangente com a reta normal!
Para a reta tangente à curva temos:
Esse é o coeficiente angular que descobrimos lá em cima, só que a gente não conhece o para termos esse resultado. Então vamos calcular pra achat :
Usando a regra da potência:
Temos:
Temos que:
Vamos achar :
Passo 3
Agora sim, podemos escrever a equação da reta tangente:
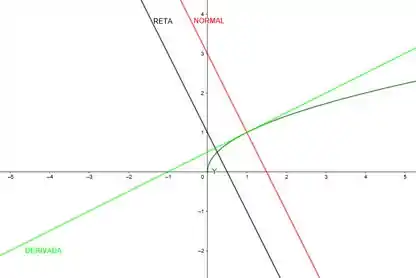
Prontinho, agora se liga nesse desenhozinho só pra ficar mais bonitinho pra vocês:
