Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.7 - Ex. 54
Encontre uma equação da reta que passa pelo ponto e que delimita a menor área do primeiro quadrante.
Passo 1
Eaee, belezinha??
Bom... queremos encontrar uma equação da reta que passa pelo ponto e que delimita a menor área do primeiro quadrante.
Para isso, primeiramente devemos colocar essas informações em um desenho:
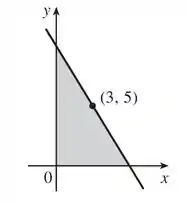
Lembre-se que a equação da reta é dada por:
Onde:
- é a coordenada do eixo vertical;
- é a coordenada do eixo horizontal;
- é a inclinação (coeficiente angular) da reta;
- são pontos conhecidos da reta.
E aí? Bora lá aplicar?? 😉
Passo 2
Chamaremos a inclinação da reta que passa pelo ponto de , e porque a inclinação dessa reta é negativa.
A equação dessa reta é:
O intercepto de é e o de é , então, a área desse triângulo é:
Tranquilo até aqui? 😉
Passo 3
Minimizando a área, ou seja, derivando e igualando a zero:
(porque a inclinação é negativa)
Substituindo o negativo nessa conta a segunda derivada fica positiva, então, a área realmente é mínima quando , e a equação da reta é:
Entendeu direitinho?? Responde Aí 😉
Resposta
Equação da reta: .