Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.1 - Ex. 47
Encontre a primeira e segunda derivada da função. Verifique se suas respostas são razoáveis comparando os gráficos de , e .
Passo 1
Fala aí! tudo certinho? 😉
Nesse problema devemos derivar a função
duas vezes para encontrar a primeira e segunda derivada e, daí esboçar seus gráficos. Por fim, precisamos compararos gráficos e ver se eles são razoáveis.
Parece de boa? 😁
Para obter as derivadas de cada termo da função, vamos usar a regra da potência
Veja só! 😊
Passo 2
A primeira derivada será
Já a segunda derivada será
Tranquilo até aqui? 😁
Passo 3
Plotando os gráficos , e
Em vermelho o gráfico de , azul o de e roxo o de :
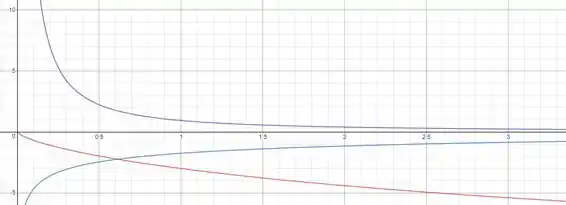
Note que como a curva azul é sempre negativa, a curva vermelha é sempre descrescnte.
Por outro lado, como a curva roxa é sempre positiva, a curva azul é sempre crescente, de modo que a curva vermelha tem sempre concavidade para cima.
Esse comportamento é bem razoável.
E aí! o que achou? Responde Aí! 😉