Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 3.4 - Ex. 55
- Encontre uma equação da reta tangente à curva
no ponto .
- Ilustre a parte (a) fazendo o gráfico da curva e da tangente na mesma tela.
no ponto .
Passo 1
Eaee, belezinha?? Bom... queremos encontrar a equação que é tangente a seguinte curva no ponto :
Para isso, temos que a equação da reta tangente é do formato:
O valor é a inclinação da reta, e é achado calculando a primeira derivada da função e aplicando o valor do ponto pedido, vamos então fazer isso aos poucos.
A questão também quer que ilustremos o que a gente vai calcular de forma que plotemos um gráfico da curva e da tangente na mesma tela.
Agora bora lá!! 😉
Passo 2
Vamos usar a regra da divisão para calcular a derivada de :
Temos que:
e
Vamos agora só montar na fórmula:
Passo 3
A derivada de é calculada usando a regra da função constante:
Passo 4
A derivada de é calculada usando a regra da função constante e regra da cadeia:
E
Assim:
Passo 5
Agora é só substituir na expressão do passo :
Passo 6
Vamos agora aplicar no ponto :
Passo 7
Agora é só substituir na fórmula da equação da reta, utilizando o ponto dado:
Passo 8
Ilustração do gráfico
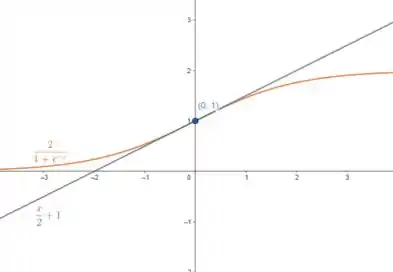
Resposta
