Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.1 - Ex. 64
Encontre as equação de ambas as retas pelo ponto que são tangentes à parábola .
Mostre que não existe nenhuma reta que passa pelo ponto que seja tangente à parábola. A seguir desenhe um diagrama pra ver por quê.
Passo 1
Oii, vamos fazer essa questão! Na letra (a) o enunciado pela pra a gente encontrar as equações das retas tangentes à parábola e que passam pelo ponto .
Antes de qualquer coisa a gente precisa se atentar a um fato! O ponto não pertence à parábola! Pois:
Beleza, dito isso vamos pensar como resolver esse problema! Pra a gente calcular a equação da reta tangente fazemos:
O é a derivada da parábola em um ponto que a gente ainda não conhece. Temos que:
Vamos substituir e na equação da reta:
Passo 2
Agora, a reta tangente tem um ponto em comum com a parábola, certo? Que é onde elas se interceptam.
Então podemos igualar essa equação que terminamos de achar com a equação da parábola pra descobrir qual valor de elas tem em comum:
Chegamos em uma equação quadrática, vamos resolve-la:
Achamos dois valores pra , isso significa que vamos ter duas retas tangentes à parábola que passam pelo ponto .
Passo 3
Podemos calcular os valores de :
Passo 4
Temos então os pontos . Podemos calcular e substituindo em:
Passo 5
Agora sim, montamos as equações das retas:
Ufaaa, uma parte foi!
Passo 6
Agora vamos para a letra (b), temos que provar que não existe nenhuma reta que passa pelo ponto que seja tangente à parábola.
Para isso vamos tentar achar uma reta que passa pelo ponto que seja tangente à parábola! Vamos usar os mesmos passos que fizemos na letra (a), só que aqui vamos mais direto, beleza?
Substituindo o ponto e na equação da reta:
Agora igualamos com a parábola pra achar o ponto de intersecção:
Opaaa...batemos em uma raíz negativa! É por isso que não existe uma reta tangente à parábola que passa por esse ponto! Afinal não existe uma solução para intersecção nos números reais!
Vamos dar uma olhada nas curvas:
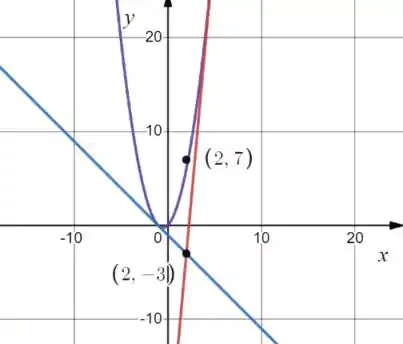
Repara que o ponto fica “dentro” da parábola! Realmente não teria como a gente ter uma reta tangente que passasse por esse ponto!