80. Esboce as parábolas e . Você acha que existe uma reta que seja tangente a ambas as curvas? Em caso afirmativo, encontre sua equação. Em caso negativo, explique por que não.

Seja a inclinação de tal reta. Sabe-se que

E tambem que

Sabe-se que, pela Geometria Analítica, a inclinação da reta pode ser dada por , sendo que e .

Então, substituindo e na expressão de teremos:

Tranquilo até aqui? 😁

Podemos fazer as seguintes igualdades:

E também

Igualando o lado direito da equação resultante com o lado direito da equação resultante . Temos que:

Também da igualdade da equações e teremos:

Formamos então um sistema com as duas últimas equações obtidas:

somando as duas equações do sistema temos e, logo, .

bacana, não é? 😎

Então, a equação da reta seria:

Onde

E

Ou seja

Simplificando...

Esboço:

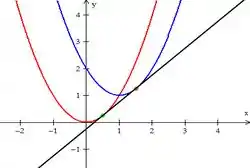
Observação: o ponto verde é o ponto de tangência da reta com a parábola e o ponto laranja é o ponto de tangência da mesma reta com a parábola .

E aí! o que achou? Responde Aí! 😉