Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 10.2 - Ex. 9
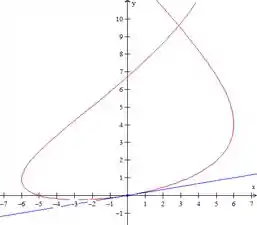
Encontre uma equação da(s) tangente(s) à curva no ponto dado. A seguir, trace a curva e a(s) tangente(s) com auxílio de uma ferramenta gráfica.
Passo 1
Opa, tudo tranquilo? A questão dá pra gente a curva definida por
E nos pede para que encontremos
No ponto
Mas como fazemos isso? A derivada (ou a equação da reta tangente) de uma curva definida por equações paramétricas é descrita da seguinte forma
Dessa forma só precisamos encontrar as derivadas de e em relação a e substituir nessa fórmula! Para encontrar o valor do parâmetro só precisamos igualar as expressões da curva ao ponto!
A questão ainda pede para que plotemos o gráfico da curva e da reta tangente em algum software! Recomendo o GeoGebra (geogebra.org/calculator).
Passo 2
Buscamos
Encontrando derivada de :
Agora a derivada de :
Substituindo na fórmula, ficamos a equação da reta tangente!
Passo 3
Temos a equação da reta tangente “genérica” dessa curva, mas para encontrar a reta no ponto precisamos encontrar o valor do parâmetro correspondente! Parra isso, igualamos as expressões ao valor delas no ponto
Daí tiramos que
Substituindo no vetor tangente, temos:
Passo 4
Assim, a equação da reta tangente no ponto fica:
Passo 5
Agora vamos traçar a curva e a nossa reta tangente no ponto .
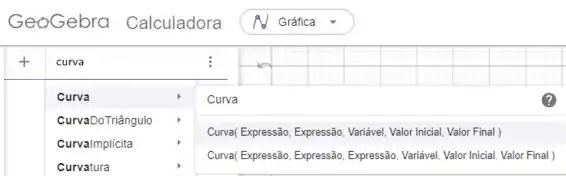
Usando a função curva do GeoGebra podemos facilmente plotar a nossa!
E para plotar a reta é mais fácil ainda! De forma que obtemos o seguinte
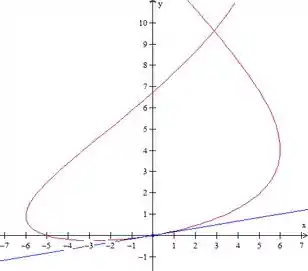
Resposta
