Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.9 - Ex. 9

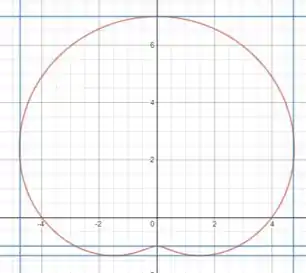
Nos exercícios 9 a 20, determine os pontos nos quais a curva dada tem retas tangentes verticais e horizontais. Faça um esboço do gráfico e mostre essas retas tangentes

9. r = 4 + 3 s e n θ

Passo 1

Como o enunciado nos pede para obtermos as retas tangentes e diz que devem ser verticais e horizontais, precisaremos calcular a inclinação das retas através da equação:

t g α = t g θ d r d θ + r d r d θ - r t g θ

Passo 2

Primeiro precisamos determinar d r d θ :

d r d θ = 3 c o s θ

Para que a reta seja horizontal, t g α precisa ser 0 e colocaremos o valor de r conforme a equação no enunciado, ficamos com:

t g α = 3 t g θ c o s θ + 4 + 3 s e n θ 3 c o s θ - 4 + 3 s e n θ t g θ = 0

Igualando somente o numerador a 0, pois o quociente passa multiplicando o zero:

3 s e n θ c o s θ c o s θ + 4 + 3 s e n θ = 0

Dividindo e multiplicando os outros termos por cosseno

3 s e n θ c o s θ c o s θ + 4 c o s θ c o s θ + 3 s e n θ c o s θ c o s θ = 0

Passando os c o s θ multiplicando o zero no outro lado:

3 s e n θ c o s θ + 4 c o s θ + 3 s e n θ c o s θ = 0

Colocando em evidência:

c o s θ 6 s e n θ + 4 = 0

Então:

s e n θ = - 2 3 → θ ≅ - 0,72   e   θ ≅ - 2,42

c o s θ = 0 → θ = π 2   e   θ = 3 π 2

Teremos então quatro pontos onde retas horizontais tangenciam nossa curva vamos determinar o valor de r primeiro para   θ ≅ - 0,72

r = 4 - 3.2 3 = 2

E com ele encontrar o ponto onde a reta horizontal cruza para θ ≅ - 0,72

y = r s e n θ = - 2 .   2 3 = - 4 3

x = r c o s θ = 2 c o s - 0,72 ≅ 1,49

Para θ ≅ - 2,42 :

y = - 4 3

x ≅ - 1,50

Para θ = π 2 :

r = 4 + 3 = 7

y = 7.1 = 7

x = 0

E para θ = 3 π 2 :

r = 4 - 3 = 1

y = 1 . - 1 = - 1

x = 0

Ou seja, as retas horizontais passam nos pontos 1,49 ,   - 4 3 , 0 ,   7 e 0 , - 1

Passo 3

Para a reta vertical precisaremos que o denominador seja 0, pois a inclinação tenderá para infinito, o que corresponde a uma reta vertical:

3 c o s θ - 4 + 3 s e n θ t g θ = 0

3 c o s θ - 4 + 3 s e n θ s e n θ c o s θ = 0

Dividindo e multiplicando o primeiro termo por c o s θ :

3 c o s 2 θ - 4 s e n θ - 3 s e n 2 θ = 0

Reescrevendo:

s e n 2 θ + 4 3 s e n θ - c o s 2 θ = 0

Substituindo c o s 2 θ por 1 - s e n 2 θ :

s e n 2 θ + 4 3 s e n θ - 1 + s e n 2 θ = 0

2 s e n 2 θ + 4 3 s e n θ - 1 = 0

s e n 2 θ + 4 6 s e n θ - 1 2 = 0

Aplicando a Fórmula de Bhaskara para o seno:

s e n θ = - 1 3 ± 2 2

Como a solução negativa é complexa, ficaremos apenas com o valor positivo:

s e n θ = 2 2 - 1 3

θ ≅ 0,38   e   θ ≅ 2,76

Substituindo na equação de r para θ ≅ 0,38 :

r = 4 + 3 2 2 - 1 3 = 3 + 3 2 2

E as coordenadas cartesianas serão:

x = r c o s θ ≅ 4,75

y = r s e n θ ≅ 1,91

E para θ ≅ 2,76 :

x = 3 + 3 2 2 c o s ⁡ ( 2,76 ) ≅ - 4,75

y = 3 + 3 2 2 s i n ⁡ ( 2,76 ) ≅ 1,91

O que significa que as retas verticais passarão aproximadamente nos pontos 4,75   ,   1,91 e ( - 4,75 ,   1,91 )

Passo 4

O esboço do gráfico será:

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos exercícios de 21 a 28, ache χ e α para a curva dada no ponto cujo valor de θ é o indicado. Faça um esboço da curva e mostre χ e α .21. r θ = 4 ; θ = 1
Nos exercícios de 21 a 28, ache χ e α para a curva dada no ponto cujo valor de θ é o indicado. Faça um esboço da curva e mostre χ e α .27. r = 3 c o s 2 θ ; θ = π 6
Nos exercícios 9 a 20, determine os pontos nos quais a curva dada tem retas tangentes verticais e horizontais. Faça um esboço do gráfico e mostre essas retas tangentes16. r = 1 - 2 s e n θ
Dada a curva r = k , onde k é uma constante não-nula e α é a medida em radianos da inclinação da reta tangente à curva no ponto r ,θ . Mostre que t g α t g θ = - 1 para todo θ tal que θ ≠ 0 .
Nos exercícios de 29 a 32, ache a medida, em graus, do menor ângulo entre as retas tangentes ao par de curvas dadas nos pontos de intersecção indicados:31. r = 4 c o s θ r = 4 c o s 2 θ - 3 ; - 2 ,2 π