Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 13.1 - Ex. 14
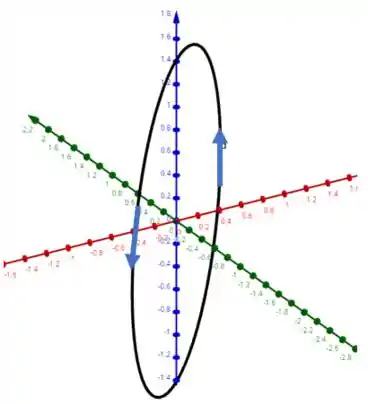
Esboce o gráfico da curva cuja equação vetorial é dada. Indique com seta a direção na qual o parâmetro cresce.
Passo 1
Eaee, belezinha?? Bom... o enunciado nos deu a seguinte função vetorial:
Primeiramente queremos esboçar o gráfico dessa função.
Para isso, devemos analisar as equações paramétricas dessa função para ver que figura tridimensional elas formam. Nesse caso, devemos saber da seguinte relação entre coordenadas e vetores unitários:
Com isso, vamos manipular algebricamente essas equações para verificarmos o padrão da equação que forma com as variáveis.
Em seguida, vamos verificar o crescimento de de acordo com a equação que estamos analisando.
Agora bora lá! 😉
Passo 2
As equações paramétricas são:
Elevando todas as componentes ao quadrado e somando, temos:
Sabemos que , portanto:
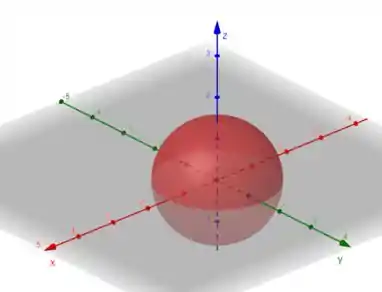
Ou seja, a curva se encontra em uma esfera centrada na origem e de raio :
Passo 3
Além disso, a segunda e terceira coordenada são iguais, indicando que a curva é a interseção da esfera encontrada no passo 2 com o plano .
Tal intercessão é o círculo de raio com centro na origem e no plano .
Esboçando, temos a seguinte figura, onde o parâmetro cresce no sentido anti-horário.
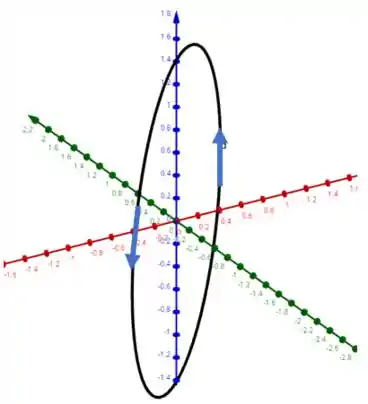
Resposta
A curva procurada é o círculo de raio com centro na origem e no plano .
