Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 1.3 - Ex. 59
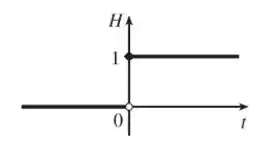
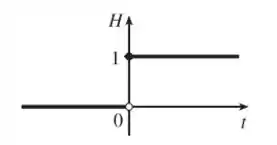
A função de Heaviside é definida por:
Essa função é usada no estudo de circuitos elétricos para representar o surgimento repentino de corrente elétrica, ou voltagem, quando uma chave é instantaneamente ligada.
- Esboce o gráfico da função de Heaviside;
- Esboce o gráfico da voltagem no circuito se uma chave for ligada no instante e volts forem aplicados instantaneamente no circuito. Escreva uma fórmula para em termos de ;
- Esboce o gráfico da voltagem em um circuito quando é ligada uma chave em segundos e volts são aplicados instantaneamente no circuito. Escreva uma fórmula para em termos de . (Observe que começar em corresponde a uma translação.)
Passo 1
Eaee, belezinha?? Bom... a questão nos dá a seguinte função:
Queremos esboçar alguns gráficos aqui.
Para ficar melhor, a cada passo abaixo a gente vai vendo um por um, certinho? 😉
Passo 2
Na letra a) o gráfico é bem simples.
Perceba que para a função é constante e igual a zero.
Já para a função tem valor constante e igual a .
Assim, plotando, temos:
Passo 3
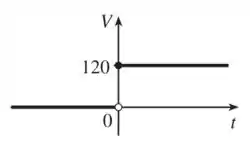
Na letra b) a questão quer que esbocemos o gráfico da voltagem no circuito se uma chave for ligada no instante e volts forem aplicados instantaneamente no circuito.
Bom... podemos descrever como:
Ou seja, temos:
Assim, plotando, temos:
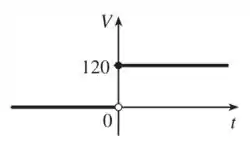
Passo 4
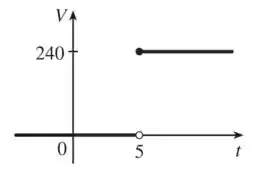
Por fim, na letra c) queremos esboçar o gráfico da voltagem em um circuito quando é ligada uma chave em segundos e volts são aplicados instantaneamente no circuito.
Matematicamente, temos:
Ou seja, temos:
Para plotar o gráfico, é interessante sabermos que começar em , corresponde a fazer um deslocamento de unidades para a direita:
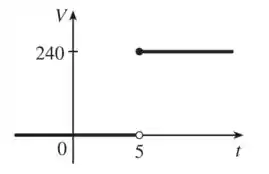
Entendeu direitinho?? Responde aee 😉
Resposta
