Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.3 - Ex. 33

Esboce a curva com a equação dada.

Passo 1

Falaee, beleza?? Bom... queremos esboçar a curva dada pela seguinte equação polar para :

Lembrando que equações polares o representa a distância do ponto até a origem e o o ângulo do ponto em relação ao eixo horizontal positivo.

Mas e para esboçar o nosso gráfico??

Bom... aí a gente tem que interpretar o que nossa equação nos quer dizer.

No nosso caso, como a distância do ponto até a origem será sempre igual à angulação.

E quanto maior o ângulo.... maior a distância!!!

Passo 2

Pensando sobre o gráfico, a medida que aumentamos o ângulo, a gente aumenta a distância.

Se não limitarmos o valor de terminaríamos com um tipo de espiral infinito.

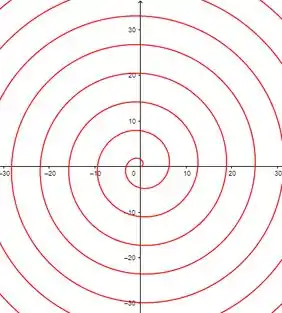
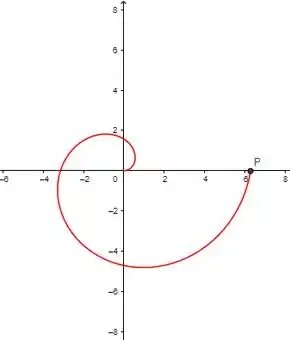
Vamos fazer dos dois jeitos, primeiramente com de à :

Se não limitarmos o ficamos com algo assim:

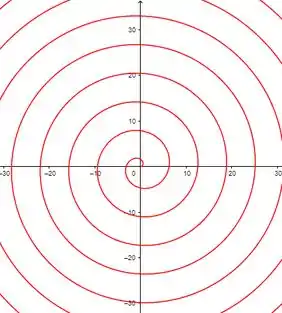
Perceba que quanto mais aumentamos o ângulo, maior se torna nossa expiral!!

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma família de curvas tem equações polares r = 1 - acos ⁡ θ 1 + a cos ⁡ θ Investigue como o gráfico muda quando a varia. Em particular, você deveria identificar, plotando a curva com uma ferramenta gr

O astrônomo Giovanni Cassini (1965-1712) estudou a família de curvas com equações polares r 4 - 2 c 2 r 2 cos ⁡ 2 θ + c 4 - a 4 = 0 Para as quais a e c são números reais positivos. Essas curvas são ch

Esboce a curva usando as equações paramétricas para marcar os pontos. Indique com uma seta a direção na qual a curva é traçada quando t aumenta.3. x = 5s e nt , y = t 2 ,- π ≤ t ≤ π

Esboce a curva usando as equações paramétricas para marcar os pontos. Indique com uma seta a direção na qual a curva é traçada quando t aumenta. x = e - t + t , y = e t - t ,- 2 ≤ t ≤ 2

Esboce a curva usando as equações paramétricas para marcar os pontos. Indique com uma seta a direção na qual a curva é traçada quando t aumenta. x = 1 + t ,y = t 2 - 4 t ,0 ≤ t ≤ 5