Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 10.3 - Ex. 34
Esboce a curva com a equação dada.
Passo 1
Olá, meu brother. Vou te ajudar a resolver essa atividade.
A gente quer esboçar a curva:
O que a equação representa?
As coordenadas polares, que você pode ver abaixo:
São representadas por o raio, que é a distância da origem até determinado ponto, e o ângulo que é a inclinação entre o raio e a horizontal.
Então o que temos aqui é uma curva onde o seu raio está em função do . Então deveremos ter vários pontos ao longo do eixo.
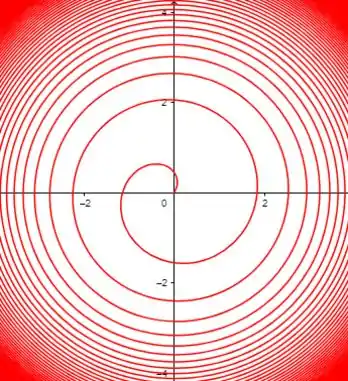
Como o está limitado a valores acima de 1, seu logaritmo vai variar de à , portanto teremos novamente um formato espiralado.
Passo 2
Diferentemente da equação de primeiro grau simples, o logaritmo a partir de tem um comportamento quase como que de uma raiz, portanto é esperado que o espiral continue até o infinito, mas cada vez mais com uma diferença de distância menor ao anterior.
Como o está limitado para valores maiores que , o nosso gráfico sairá da origem, pois . Vamos construir o gráfico utilizando o GeoGebra, para maior precisão nos nossos resultados.
Mas você pode fazer o seguinte, criar uma tabela com os valores de , e assim criar um esboço do gráfico com diversos pontos:
No gráfico gerado pelo GeoGebra, se limitarmos o :
Se deixarmos o :
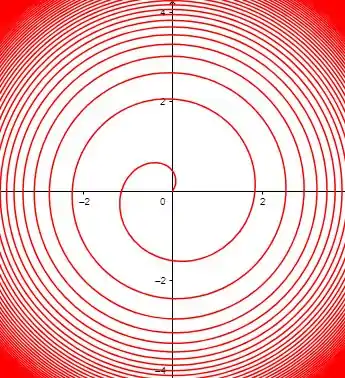
Resposta
