Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 3.6 - Ex. 48
Encontre o erro nos seguintes cálculos:
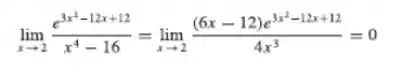
E em seguida encontre a resposta crreta:
Passo 1
Logo de cara, ao subistituirmos o valor do limite na função encontramos , ou seja,. Essenão é uma valor elegível a se aplicar l’hospital.
Passo 2
O correto então seria:
Resposta
Exercícios de Livros Relacionados
Faça uma conjectura sobre o limite traçando o gráfico da função envolvida com um recurso computacional; verifique sua conjuctura usando a regra de L’Hôpital. lim x → 0 + s e nx 3 ln x
Se não utilizássemos a Regra de L’Hôpital para calcular lim x → 0 sen x x ou lim x → + ∞ 1 + 1 x x poderíamos ser acusados de raciocínio circular. Explique por quê.
Suponha que as funções f e g sejam diferenciáveis em x = a e que f a = g a = 0 . Se g ' a ≠ 0 , mostre que lim x → a f x g x = f ' a g ' a sem usar a regra de L’Hôpital. [Sugestão: Divida o numerado
Há um mito que circula entre os que começam estudar Cálculo de que todas as formas indeterminadas dos tipos 0 0 ,∞ 0e1 ∞ são iguais a 1 , pois “qualquer coisa elevada a zero é 1 ” e “ 1 a qualquer pot
Há um mito que circula entre os que começam estudar Cálculo de que todas as formas indeterminadas dos tipos 0 0 ,∞ 0e1 ∞ são iguais a 1 , pois “qualquer coisa elevada a zero é 1 ” e “ 1 a qualquer pot