Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.6 - Ex. 5
Escreva a equação polar da cônica com o foco na origem e com as informações dadas
5. Elipse, excentricidade , vértice
Passo 1
Olá, meu amigo. A gente vai resolver essa atividade juntos aqui hoje.
Precisamos escrever a equação na forma polar de uma elipse de excentricidade de e com o vértice em:
A equação polar para uma cônica é dada por:
Ou
Podemos ver abaixo como se comporta cada uma:
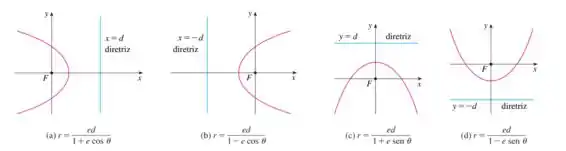
As coordenadas do vértice dadas no enunciado, nos mostram que o vértice está à esquerda do foco que está na origem, ou seja, a diretriz que fica do lado da elipse, será vertical e negativa, então precisamos colocar no denominador na equação da cônica, ficando com:
Passo 2
Substituímos então o valor dado da excentricidade e a coordenada do vértice para encontrarmos :
Isolando :
Passo 3
Substituindo o valor que encontramos e a excentricidade, a equação vai ficar: