Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 1.1 - Ex. 56
Encontre uma expressão para a função cujo gráfico é a curva dada:
Passo 1
E aí! tudo certinho? 😇
Nesse problema queremos determinar a função que descreve o gr��fico dado por
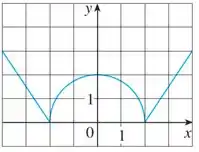
Parece complicado? 🤔
Bom pessoal, o segredo dessa questão é dividir o gráfico em três partes: a primeira é a reta mais à esquerda, a segunda o semi-círculo no meio e a terceira a outra reta mais à direita, ta bom?
Bora lá! 👀
Passo 2
Nessa primeira parte, vamos pegar os pontos e para jogar na nossa equação da reta, dada por:
Substiuindo os valores, vamos ter:
Organizando os sinais na equação, vamos ter:
Continuando:
E aí achamos a expressão da primeira parte do nosso gráfico! Essa expressão vai existir só no intervalo , ta bom?
Tranquilo até aqui? 😁
Passo 3
Vemos que a segunda parte do nosso gráfico é a metade superior de uma circunferência de raio . A equação de uma circunferência (quando ela ta com o centro na origem do gráfico) é:
A gente vai ter então que a nossa equação vai ficar:
Agora, nós termos que escrever em termos de . Olha só como a gente faz isso:
Tirando a raiz dos dois lados:
Podemos ter uma raíz negativa ou positiva para um mesmo número, tranquilo? Não vai esquecer! Por esse motivo, a gente colocou o mais e menos na frente da raíz. Acontece que a expressão negativa seria a parte inferior da circunferência, enquanto a expressão positiva é a parte de cima. Logo, sabemos que a expressão que a gente quer é:
Ah, antes que eu me esqueça: isso só vale no intervalo !
Bora continuar! 😉
Passo 4
Falta só mais uma parte do gráfico galera! E nessa aqui a gente faz a mesma coisa que fez no passo , so vai ter que pegar outros pontos. Nesse caso, a gente vai usar e . Saca só:
O que vai dar:
Que, fazendo a multiplicação:
Pronto, achamos a expressão da nossa última parte! Ela é válida só para . Dessa forma, a nossa função, que chamaremos de , vai ficar:
Dá uma olhada que, da primeira para a segunda condição de existência, tem um “” e não um “” no . Isso é só uma questão de notação mesmo (você deve colocar um símbolo em uma condição e o outro símbolo na outra, independente da ordem). O mesmo vale quando vamos da segunda condição para a terceira, com relação ao .
Não vai esquecer disso quando for escrever a sua resposta, combinado? ;)
Entendeu tudo? Responde Aí! 😬
