Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.2 - Ex. 66

Encontre os extremos relativos no intervalo 0 < x < 2 π e confirme se seus resultados estão de acordo com o gráfico gerado por um recurso computacional.

f x = sen ⁡ x 2 - cos ⁡ x

Passo 1

Para achar os pontos relativos de f x vamos encontrar a primeira derivada:

f ' x = cos ⁡ x 2 - cos ⁡ x - sen ⁡ x 0 - - sen ⁡ x 2 - cos ⁡ x 2 = 2 cos ⁡ x - cos 2 ⁡ x - sen 2 ⁡ x 2 - cos ⁡ x 2 =

= 2 cos ⁡ x - cos 2 ⁡ x + sen 2 ⁡ x 2 - cos ⁡ x 2 = 2 cos ⁡ x - 1 2 - cos ⁡ x 2

Fazendo f ' x = 0 vamos ver se possui algum ponto crítico, onde a derivada é zero, ou onde ela não existe:

2 cos ⁡ x - 1 2 - cos ⁡ x 2 = 0 → 2 cos ⁡ x - 1 = 0 → cos ⁡ x = 1 2

Temos como pontos críticos então:

x = π 3

x = 5 π 3

Passo 2

Agora vamos usar o teste da segunda derivada, vamos calcular f ' ' x :

f ' ' x = 2 - sen ⁡ x - 0 2 - cos ⁡ x 2 - 2 cos ⁡ x - 1 2 2 - cos ⁡ x 0 - - sen ⁡ x 2 - cos ⁡ x 4 =

= - 2 sen ⁡ x 2 - cos ⁡ x 2 - 2 2 cos ⁡ x - 1 2 - cos ⁡ x sen ⁡ x 2 - cos ⁡ x 4 =

= - 2 sen ⁡ x 2 - cos ⁡ x - 2 2 cos ⁡ x - 1 sen ⁡ x 2 - cos ⁡ x 3 =

= - 4 sen ⁡ x + 2 sen ⁡ x cos ⁡ x - 4 sen ⁡ x cos ⁡ x + 2 sen ⁡ x 2 - cos ⁡ x 3 = - 2 sen ⁡ x - 2 sen ⁡ x cos ⁡ x 2 - cos ⁡ x 3 =

= - 2 sen ⁡ x 1 + cos ⁡ x 2 - cos ⁡ x 3

Vamos usar o Teste da Derivada Segunda:

Se f ' x 0 = 0 e f ' ' x 0 > 0 , então f tem um mínimo relativo em x 0 .

Se f ' x 0 = 0 e f ' ' x 0 < 0 , então f tem um máximo relativo em x 0 .

Se f ' x 0 = 0 e f ' ' x 0 = 0 , então o teste é inconclusivo, isto é, f pode ter um máximo ou mínimo relativo em x 0 ou nenhum dos dois.

Vamos então achar os valores das segundas derivadas nos pontos críticos, e analisar os sinais:

f ' ' π 3 = - 2 sen ⁡ π 3 1 + cos ⁡ π 3 2 - cos ⁡ π 3 3 = - 2 ⋅ 3 2 1 + 1 2 2 - 1 2 3 = - 3 ⋅ 3 2 3 2 3 < 0

f ' ' 5 π 3 = - 2 sen ⁡ 5 π 3 1 + cos ⁡ 5 π 3 2 - cos ⁡ 5 π 3 3 = - 2 ⋅ - 3 2 1 + 1 2 2 - 1 2 3 = 3 ⋅ 3 2 3 2 3 > 0

Pelo Teste da Derivada Segunda temos que x = π 3 é um máximo relativo e x = 5 π 3 é um mínimo relativo.

Passo 3

Vamos agora conferir pelo gráfico:

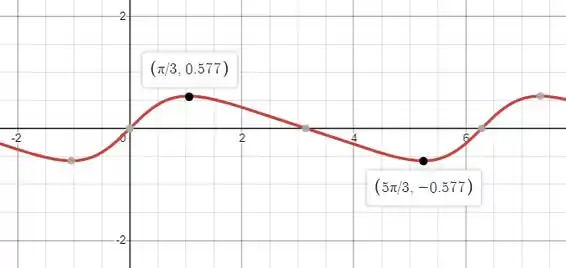
Por ele conseguimos ver que temos que x = π 3 como um máximo relativo e x = 5 π 3 como mínimo relativo.

Resposta

x = π 3 é um máximo relativo e x = 5 π 3 é um mínimo relativo

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

É dada uma fórmula para a derivada de uma função. Quantos números críticos ela tem? f ' x = 100 cos 2 ⁡ x 10 + x 2 - 1
Encontre os valores de máximo e mínimo absoluto de f no intervalo dado f x = x 3 - 3 x + 1 , [ 0,3 ]
É dada uma fórmula para a derivada de uma função. Quantos números críticos ela tem? f ' x = 5 e - 0,1 x sin ⁡ x - 1
Encontre os números críticos da função s t = 3 t 4 + 4 t 3 - 6 t 2
Encontre os números críticos da função g y = y - 1 y 2 - y + 1