Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 4.1 - Ex. 28
Encontre o gráfico esboçado da função f e ache os valores de máximos e mínimos absolutos e locais.
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você??Vamos analisar o que nosso probleminha está falando. Bom, ele nos pede para montar um gráfico baseado nessa função e apresentar nossos máximos e mínimos locais e absolutos.
Nosso primeiro passo vai ser analisar nossa função para cada um dos extremos definidos ali.
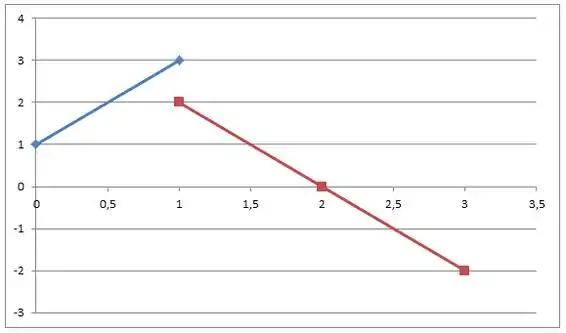
Ok, vamos começar ali no 0. No intervalo fechado em 0 e aberto em 1, temos uma função linear crescente. Agora, vamos analisar nossa segunda restrição da função. Com o intervalo fechado entre 1 e 3, temos uma função linear decrescente.
Passo 2
Para esboçar o gráfico da função podemos dividir a função em dois intervalos:
1. Para
2. Para
Agora, podemos esboçar o gráfico
- No intervalo a função é uma linha reta com inclinação positiva. Ela passa pela origem e sobe para a direita.
- No intervalo a função também é uma linha reta, mas com inclinação negativa. Ela começa em (1,2) e desce para a direita.
Passo 3
Agora, vamos encontrar os valores de máximos e mínimos absolutos e locais.
Máximos e mínimos absolutos:
- Para encontrar os máximos e mínimos absolutos, primeiro calculamos os valores da função nos extremos do domínio e nos pontos críticos dentro do domínio.
- Extremos do domínio:
- Pontos críticos (onde a derivada é zero ou indefinida):
- Como é linear em ambos os intervalos, não há pontos críticos dentro do domínio.
- Comparando os valores, o máximo absoluto é e o mínimo absoluto é
Máximos e mínimos locais:
- Como a função é uma sequência de segmentos de reta, ela não possui máximos ou mínimos locais dentro dos intervalos fornecidos.
Passo 4
Portanto, os valores de máximos e mínimos absolutos são:
- Máximo absoluto: alcançado em
- Mínimo absoluto: alcançado em
Aqui está o esboço do gráfico:
Resposta
- Máximo absoluto: alcançado em
- Mínimo absoluto: alcançado em