Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 4.1 - Ex. 64
Use um gráfico para estimar os números críticos de
Com precisão de uma casa decimal
Passo 1
Oieee, bora resolver junto comigo essa RA
Simboraaaa
O enunciado já nos pede para resolver a questão utilizando um gráfico, existe inúmeros softwares para gerarmos esse gráfico, porém iremos utilizar o mais comum da cadeia que e o nosso amigo salvador de toda a pátria geogebra rs:
Nossa função dada pelo enunciado é :
Gráfico:
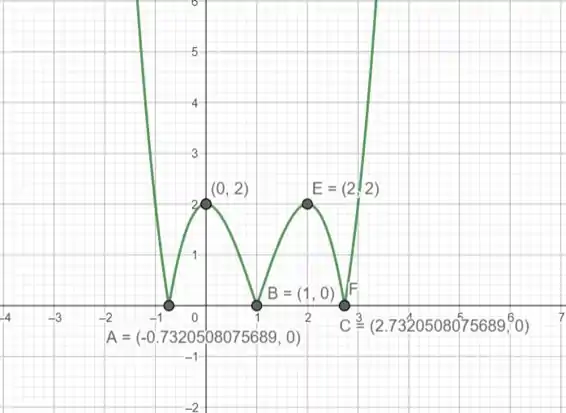
Agora podemos resolver a questão..
Simboraaa
Passo 2
Para encontrar os números críticos da função
Precisamos analisar tanto a função quanto a função resultante após aplicar o valor absoluto.
Vamos iniciar encontrando os Pontos Críticos da Função Dentro do Valor Absoluto
Primeiro, analisamos a função
Encontrar os pontos críticos resolvendo
Passo 3
Agora iremos determinar Onde Muda de Sinal
Os pontos onde muda de sinal são importantes porque o valor absoluto pode introduzir novos pontos críticos. Vamos verificar os valores de nesses pontos:
Para
Para
Os pontos críticos da função absoluta ocorrerão nos zeros de e nos pontos onde tem pontos críticos, ou seja, onde a derivada muda de sinal.
Passo 4
Vamos encontrar os Zeros de
Encontrar onde
Fatorando a equação cúbica:
Assim, um zero é Para os outros dois zeros, resolvemos a equação quadrática:
Usando a fórmula quadrática:
Portanto, os zeros de são:
Passo 5
Vamos verificar os Zeros e Pontos Críticos no Gráfico de
Os pontos críticos de serão onde a derivada da função é zero ou onde a função dentro do valor absoluto cruza o eixo x.
Lista de possíveis pontos críticos:
Passo 6
Esboço do Gráfico para Precisão de uma Casa Decimal
1. Plotar
2. Identificar onde cruza o eixo x.
3. Plotar a função e verificar onde há mudanças na inclinação (pontos críticos).
Baseado no gráfico e na análise acima, os pontos críticos aproximados de são:
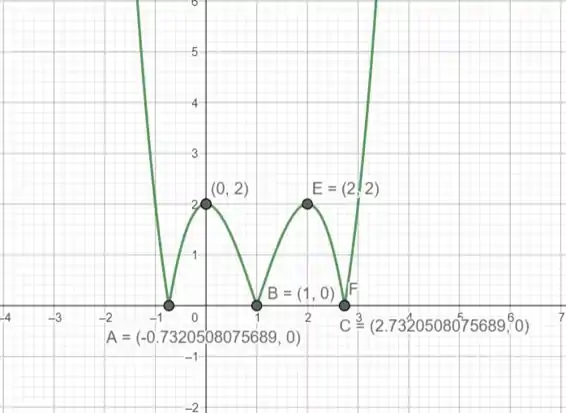
Resposta
Os números críticos da função são