Enunciado

Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 4.1 - Ex. 27

Encontre o gráfico esboçado da função f e ache os valores de máximos e mínimos absolutos e locais.

Passo 1

Oi oi, meu xuxuzinho!! Tudo bem com você??Vamos analisar o que nosso probleminha está falando. Bom, ele nos pede para montar um gráfico baseado nessa função e apresentar nossos máximos e mínimos locais e absolutos.

Nosso primeiro passo vai ser analisar nossa função para cada um dos extremos definidos ali.

Ok, vamos começar ali no -1. No intervalo fechado de -1 a 0, temos uma função parabólica clássica. Agora, vamos analisar nossa segunda restrição da função. Com o intervalo aberto em 0 e fechado em 1, temos uma função linear.

Passo 2

Vamos esboçar o gráfico da função definida por partes e encontrar os valores máximos e mínimos absolutos e locais. A função é dada por:

Para

- Esta é uma parábola voltada para cima, com vértice em onde

Para

- Esta é uma linha reta decrescente com intercepto y em e inclinação de

- No ponto de transição

- À esquerda (incluindo ), temos

- À direita, temos

- Portanto, existe uma descontinuidade em onde o valor salta de

Passo 3

Valores de nos Pontos Críticos

- No intervalo

-No intervalo

Máximos e Mínimos Locais e Absolutos

- Máximos Locais:

- Para o valor máximo local ocorre em onde

- Mínimos Locais:

- Para o valor mínimo local ocorre em onde

- Máximo Absoluto:

- O valor máximo absoluto da função ocorre em porque é o maior valor que a função atinge.

- Mínimo Absoluto:

- O valor mínimo absoluto da função ocorre em

Passo 4

Esboço do Gráfico

Vamos esboçar o gráfico das duas partes da função

1. Para O gráfico é uma parábola de vértice em

2. Para O gráfico é uma linha reta decrescente de

Gráfico

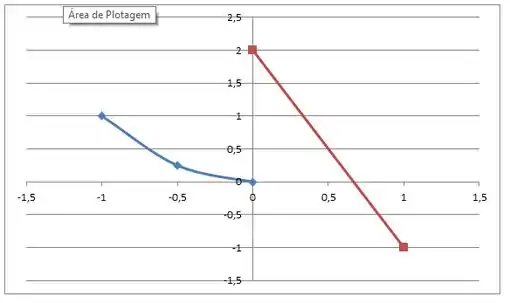
- Máximo Absoluto:

- Mínimo Absoluto:

- Máximo Local:

- Mínimos Locais:

Assim, o gráfico da função tem uma descontinuidade em e as partes contínuas da função mostram os máximos e mínimos locais e absolutos conforme descrito.