Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.1 - Ex. 65
- Use um gráfico para estimar os valores de máximo e mínimo absolutos da função com duas casas decimais.
- Use o cálculo para encontrar os valores de máximo e mínimo exatos.
Passo 1
Oi, oi... vamos que vamos! Nessa questão temos a seguinte função:
Que é dada no intervalo:
E queremos encontrar no gráfico qual o seu valor máximo e mínimo absoluto dentro do intervalo dado. Aí é basicamente olhar o gráfico e ver onde está o máximo e o mínimo da função dentro do intervalo.
Depois vamos usar o cálculo para encontrar esses pontos.
Para isso, vamos derivar a função e igualar a zero:
Os pontos de que a derivada é zero são possíveis pontos de máximo e mínimo.
Depois que encontrarmos eles, vamos substituir o na função para encontrar seus valores .
Depois vamos substituir o valor dos intervalos na função e encontrar seus valores também, pois o máximo e o mínimo podem estar na extremidade do intervalo.
Por fim, com todos os valores encontrados, vamos verificar qual é o máximo e qual é o mínimo.
Bora lá
Passo 2
Pra inicio de resolução devemos plotar um gráfico para a função. Então é só escolhermos alguns pontos para e acharmos o . Certinho??
O gráfico se comporta da seguinte forma:
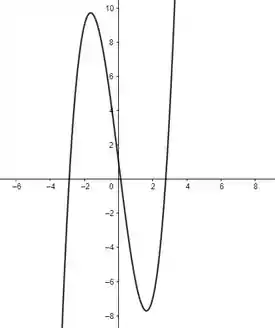
Pelo gráfico, parece que o valor máximo absoluto é cerca de e o valor absoluto mínimo é .
(para encontrar esses valores com duas casas decimais eu tive que dar um zoom no gráfico.)
Passo 3
Agora, por meio do calculo, primeiro derivamos a função:
Queremos igualar a derivada a zero, logo:
De forma que:
Usando uma calculadora, vemos que esse ponto é aproximadamente:
Aplicamos os valores onde a derivada é zero na função, logo:
E:
E por fim, aplicamos os valores do intervalo na função:
E:
Como entre os valores encontrados, o maior é e o menor é esses são o máximo e o mínimo absoluto, respectivamente.
Resposta
- o valor máximo absoluto é cerca de e o valor absoluto mínimo é ;
- O valor máximo absoluto é:
E o valor mínimo absoluto é: