Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.8 - Ex. 15
Seja .
(a) Mostre que não há num intervalo um ponto tal que , embora .
(b) Explique por que o resultado de (a) não viola o Teorema de Rolle.
Passo 1
(a) Primeiro, vamos olhar para o gráfico de para termos uma ideia melhor do que está acontecendo nesse intervalo :
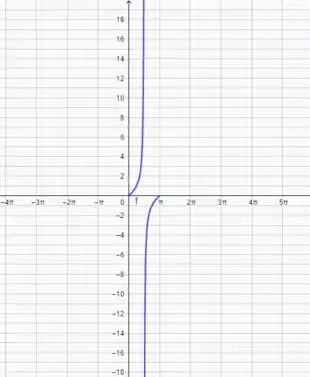
Repare que quando , a tangente não existe, pois ela explode para o infinito. Isso é muito bem apresentado pelo gráfico acima. Então, por mais que , conseguimos ver no gráfico que não tem um ponto sequer em que a derivada seja zero!
Passo 2
(b) Para que satisfaça o Teorema de Rolle, a função precisa ser contínua no intervalo fechado e derivável no intervalo aberto. Mas, como vimos no passo anterior, a função não é nem contínua nem derivável no intervalo, por conta desse salto em . Por isso, o resultado na letra anterior não viola o Teorema de Rolle.
Resposta
Explicações e demonstrações no passo a passo.