Encontre: (a) os intervalos nos quais é crescente, (b) os intervalos nos quais é decrescente, (c) os intervalos abertos nos quais é côncava para cima, (d) os intervalos abertos nos quais é côncava para baixo, (e) as coordenadas de todos os pontos de inflexão.
23.
Passo 1
Podemos responder sem grandes dificuldades todos os itens apenas analisando o gráfico:
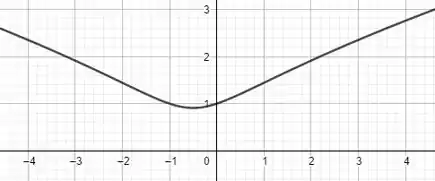
Passo 2
(a)Aqui, pra determinarmos o ponto em que começa a ser crescente, precisamos encontrar os pontos em que a derivada da função se anula (pontos de mínimo e de máximo).
A partir disso, visualizando o gáfico, determinamos os pontos iniciais dos intervalos em que a função cresce. Teremos:
Ao observar pelo gráfico então, a função passa a crescer em , ponto de mínimo, até (+) infinito. É o intervalo:
Passo 3
(b) é decrescente desde (-) infinito até . O intervalo será:
Passo 4
(c) tem concavidade voltada pra cima a partir do primeiro ponto de inflexão em , até o segundo ponto de inflexão em , quando depois volta à concavidade pra baixo. Logo, o intervalo será:
Passo 5
(d) é côncava pra baixo desde (-) infinito até o primeiro ponto de inflexão em . Volta a ter concavidade voltada pra baixo no segundo ponto de inflexão em , até (+) infinito. Logo, o intervalo é
Passo 6
(e)Os pontos de inflexão se calculam igualando a derivada segunda da função a zero. Teremos:
São esses os pontos em que a função muda de concavidade.
Resposta
Ei, a resposta está no passo a passo :)