Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 15.8 - Ex. 10

a) Encontre o jacobiano da transformacao x = u, y = uv e esboce a regiao G: 1 ≤ u ≤ 2, 1 ≤ uv ≤ 2, no plano uv.

b) Em seguida, utilize a Equacao 1 para transformar a integral

∫ 1 2 ∫ 1 2 y x   d y   d x

em uma integral sobre G e calcule ambas as integrais.

Passo 1

Faaaaalaaa meus abençoados, tudo blz?

na letra (a) vamos ter que encontrar o jacobiano da transformação que vai ficar assim,

∂ x , y ∂ u , v = J u , v =   1 0 v u = u

Agora esboçando o gráfico da região G ele fica,

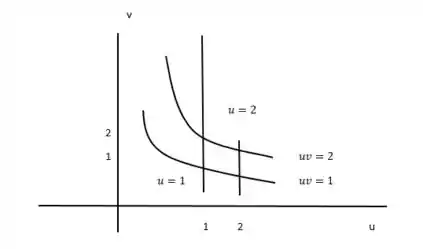
Passo 2

Já na letra (b) sendo,

x = 1 → u = 1 y = 1 → u v = 1 → v = 1 u

x = 2 → u = 2 y = 2 → u v = 2 → v = 2 u

Com isso vamos ter que,

∫ 1 2 ∫ 1 2 y x   d y   d x =   ∫ 1 2 ∫ 1 u 2 u u v u u   d v d u =   ∫ 1 2 ∫ 1 u 2 u u v   d v d u =   ∫ 1 2 u v 2 2 1 u 2 u =   ∫ 1 2 u 2 u 2 - 1 2 u 2 d u = 3 2   ∫ 1 2 u 1 u 2 d u = 3 2   ln ⁡ u 1 2 = 3 2 ln ⁡ 2  

Resposta

3 2 ln ⁡ 2  

Exercícios de Livros Relacionados

a) Resolva o sistema u = x + 2y, v = x – y para x e y em termos de u e y. Em seguida, encontre o valor do jacobiano ∂(x, y)/∂(u, y).b) Encontre a imagem pela transformacao u = x + 2y, v = x – y da reg
a) Resolva o sistema u = 2x – 3y, v = –x + y , para x e y em termos de u e v. Em seguida, encontre o valor do jacobiano ∂(x, y)/∂(u, v).b) Encontre a imagem pela transformacao u = 2x – 3y, v = –x + y
Calcule as integrais nos Exercícios 7-20. ∫ 0 π   ∫ 0 π   ∫ 0 π   c o s ⁡ ( u + v + w ) d u d v d w ( espaço u v ) ç
Calcule as integrais nos Exercícios 7-20. ∫ 0 7   ∫ 0 2   ∫ 0 4 - q 2   q r + 1 d p d q d r (espaço p q r ) ç
Calcule as integrais nos Exercícios 7-20. ∫ 0 1   ∫ 0 1 - x 2   ∫ 3 4 - x 2 - y   x d z d y d x