Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 15.8 - Ex. 04

a) Resolva o sistema u = 2x – 3y, v = –x + y , para x e y em termos de u e v. Em seguida, encontre o valor do jacobiano ∂(x, y)/∂(u, v).

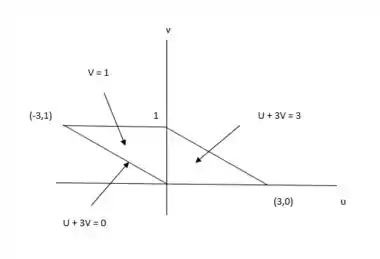
b) Encontre a imagem pela transformacao u = 2x – 3y, v = –x + y do paralelogramo R no plano xy com fronteiras x = –3, x = 0, y = x e y = x + 1. Esboce a regiao transformada no plano uv.

Passo 1

Faaaaalaaa meus abençoados, tudo blz?

Então vamos resolver primeiro o sistema dado na letra (a) em que

u = 2 x - 3 y

v = - x + y

Com isso,

- x = u + 3 v   →     x = - 1 - 3 v

y = v + x →   y = - u - 2 v

Agora resolvendo o jacobiano vamos ficar com ,

∂ x , y ∂ ( u , v ) = - 1 - 3 - 1 - 2 = 2 - 3 = - 1

Passo 2

Já na letra (b) ele pede para achar a imagem pela transformação u = 2x – 3y, v = –x + y do paralelogramo R no plano xy com fronteiras x = –3, x = 0, y = x e y = x + 1.

Sendo x = - 3 ficando - u - 3 v = 3     o u     u + 3 v = 3

x = 0 → u + 3 v = 0

y = x → v = 0

y = x + 1 → v = 1

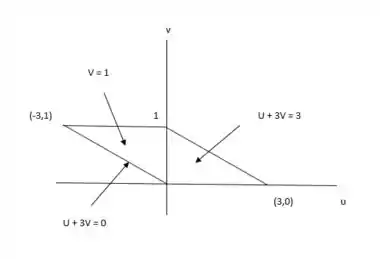
Resposta

u + 3 v = 3

u + 3 v = 0

Exercícios de Livros Relacionados

Substituições em integrais de uma variável Como as substituições em integrais definidas de uma variável podem ser vistas como transformações de regiões? Qual é o jacobiano nessecaso? Ilustre com um ex
Encontre o jacobiano ∂(x, y)/∂(u, y) da transformação:a. x = u cos y, y = u sen yb. x = u sen y, y = u cos y.
Seja D a região no espaço x y z definida pelas desigualdades 1 ≤ x ≤ 2 ,0 ≤ x y ≤ 2 ,0 ≤ z ≤ 1 . Calcule ∭ D   x 2 y + 3 x y z d x d y d z aplicando a transformação u = x ,v = x y ,w = 3 z e integrand
Utilize a transformação x = u / v , y = u v para calcular a soma integral ∫ 1 2   ∫ 1 / y y   x 2 + y 2 d x d y + ∫ 2 4   ∫ y / 4 4 / y   x 2 + y 2 d x d y
Momento de inércia polar de uma placa elíptica Uma placa fina de densidade constante cobre a região delimitada pelaelipse x2/a2 + y2/b2 = 1, a0, b0, no plano xy. Encontre oprimeiro momento da placa em