Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 2.2 - Ex. 32
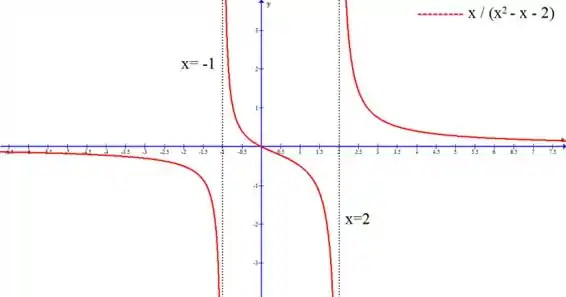
- Encontre as assíntotas verticais da função
- Confirme sua resposta da parte fazendo o gráfico da função.
Passo 1
Olá, meu querido e nobre amigo. Yuri aqui, expert do Responde Aí, e estarei aqui para te ajudar a resolver essa atividade.
O enunciado é bem direto e reto sobre o que ele quer da gente, precisamos encontrar as assíntotas verticais da função e depois confirmar a nossa resposta olhando o gráfico da função. Temos assíntotas verticais, horizontais e inclinadas (oblíquas).
As assíntotas verticais, que são as que iremos encontrar aqui, são linhas verticais que a função se aproxima à medida que a variável independente se aproxima de um valor específico.
Em outras palavras, temos uma assíntota em , se a função vai pro infinito (positivo ou negativo) quando tende a :
Geralmente onde a função possui uma descontinuidade, como um ponto onde o denominador se anula.
Pois veja bem, se temos uma função como
Qual valor dessa função que podemos nos aproximar, mas nunca poderemos encostar, e consequentemente seu limite irá tender ao infinito?
justamente sua assíntota vertical. Então o que iremos fazer aqui nessa questão é a mesma análise, iremos procurar pontos de descontinuidade ou pontos onde o denominador da nossa função se aluna, que são pontos onde o limite da nossa função tende ao infinito.
Passo 2
Letra a)
Primeiro de tudo, iremos então fatorar nosso denominador, e assim iremos visualizar melhor os pontos onde ele se anula:
Aplicando Bashkara:
Encontrando as raízes
Agora vamos analisar nossa função:
Quais pontos podem levar ao infinito o limite dessa função?
Vamos agora então calcular os limites dessa função utilizando os valores de , que encontramos. Iremos calcular os limites laterais dessa função, pois assim saberemos para quais sentidos, positivos e negativos do eixo , nossas assíntotas vão.
Passo 3
Então temos o cálculo do limite lateral , e o que acontece com o termo é que teremos uma divisão de por um valor infinitesimalmente pequeno, já que é um valor tão próximo de quanto quisermos, mas não e maior que ele
Substituindo na equação teremos o termo , que vem de , onde ser infinitesimalmente maior ou menor que não faz diferença, e que por ser constante pode sair do limite.
Isso significa que quando nos aproximarmos a por valores infinitesimalmente maior que nossa função irá ‘explodir’ para valores grandes positivos, mas nunca irá chegar na reta
Agora para
Substituindo na equação teremos o termo , que vem de e que por ser constante pode sair do limite, e uma análise análoga ocorre em torno do termo , porém agora somos infinitesimalmente menores que .
Isso significa que quando nos aproximarmos a por valores infinitesimalmente menor que nossa função irá ‘explodir’ para valores grandes negativos, mas nunca irá chegar na reta
Passo 4
Iremos fazer o mesmo agora para :
A explicação para o comportamento do infinito é a mesma para o que fizemos anteriormente.
Agora para
Com tudo que nos foi demonstrado, sabemos então que temos duas assíntotas verticais, em
Passo 5
Letra b)
Agora vamos de gráficos, vou utilizar o GeoGebra para que possamos visualizarmos se o que fizemos está correto:
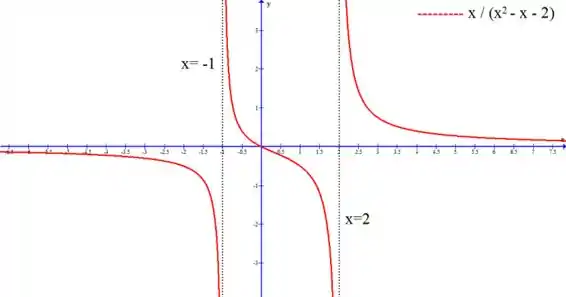
Veja que nossas conclusões sobre os sentidos de crescimento em relação as assíntotas e os valores das nossas assíntotas estão corretos.
Nos pontos de descontinuidade da função, quando o denominador se anularia, ela não está definida e explode pro infinito.
É isso, um forte abraço e até a próxima.
Resposta
