Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.6 - Ex. 3
Para a função cujo gráfico é dado, diga quem são.
a)
b)
c)
d)
e) As equações das assíntotas
Passo 1
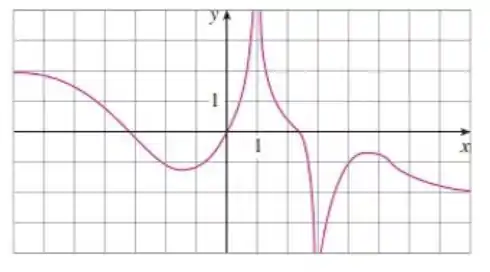
Opa, bora resolver esse problema?! Temos o seguinte gráfico:
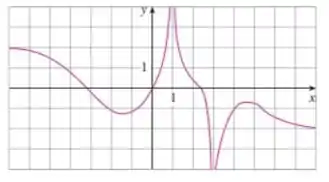
E com base nele a gente tem que identificar os limites:
Aqui é muito simples, a gente vai olhar o gráfico e ver como é o comportamento dele quando tende a esses valores.
Por fim, iremos dar a equação das assíntotas lembrando que:
Assíntota horizontal são os valores de para o qual a função tende quando ela vai para mais ou menos infinito.
Assíntota vertical são os valores de para o qual a função tende para mais ou menos infinito.
Bora lá?!
Passo 2
Começando pela letra (a)
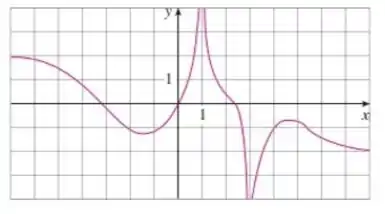
Pro maior valor de mostrado no gráfico a curva se aproxima de , então:
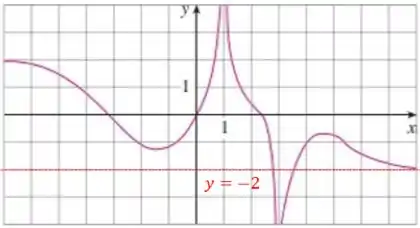
Na letra (b) temos , então vamos olhar os valores negativos extremo de :
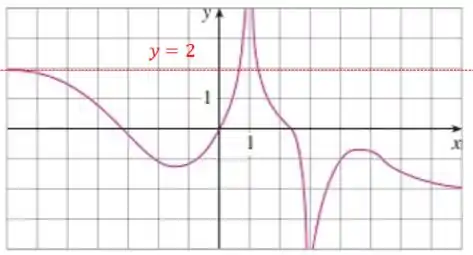
Para a letra (c) temos , então vamos acompanhar a curva quando ela se aproxima de .
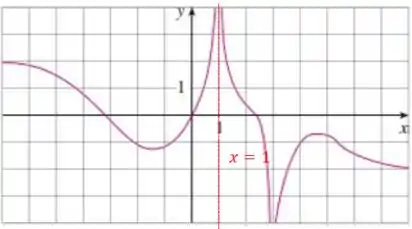
Temos então:
E finalmente a letra (d) , quando se aproxima de temos valores altos negativos pra , então:
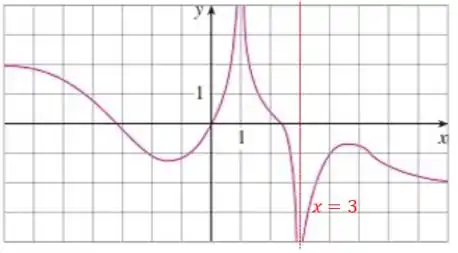
Passo 3
Agora vamos escrever as equações das assíntotas! Não tem mistério também, pra ficar mais visual eu vou desenhar elas nos gráficos:
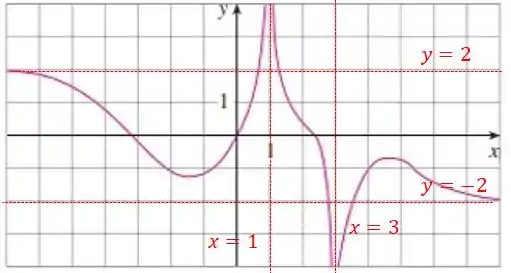
Temos duas assíntotas verticais:
E duas assíntotas horizontais:
Resposta
- .