Para a função cujo o gráfico é dado, determine o que se pede
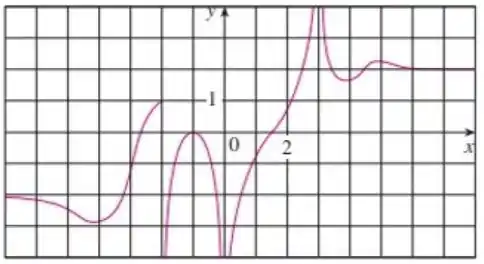
Passo 1
Bom galera, nesse exercício queremos encontrar os valores pedidos com base no gráfico dado na questão!
Temos que encontrar:
Observando esse gráfico aqui:
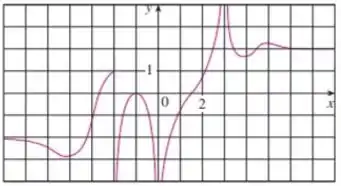
Aqui é muito simples, a gente vai olhar a expressão identificar o na curva. Bora lá?!
Passo 2
Começando pela letra . Olhando para o gráfico, podemos ver que conforme o valor de se aproxima de , o valor de se aproxima de, portanto o limite quando nossa função tende a é . Portanto:
Na letra (b) olhando para o gráfico, podemos ver que conforme o valor de se aproxima de , o valor de se aproxima de , portanto o limite quando nossa função tende a é .
Conforme o valor de se aproxima de , o valor de se aproxima de infinito, portanto o limite quando nossa função tende a , na letra c, é .
Olhando para o gráfico, podemos ver que conforme o valor de se aproxima de , o valor de se aproxima de , portanto o limite quando nossa função tende a é .
Finalmente a letra (e), podemos ver que conforme o valor de se aproxima de pela direita, o valor de se aproxima de , portanto o limite quando nossa função tende a pela direita é .
Passo 3
Agora vamos definir as equações das assíntotas, pra ficar mais fácil de visualizar, vamos desenhar no gráfico:
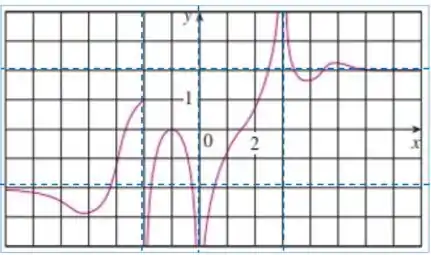
Temos as assíntotas verticais:
E as assíntotas horizontais:
Prontinho!!!
Resposta
; ; ; ; .