Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.6 - Ex. 62
Encontre os limites quando . Use essa informação, bem como as interseções com os eixos, para fazer um esboço do gráfico.
Passo 1
Olá, meu nobre amigo. Yuri aqui e estarei te ajudando a resolver essa atividade. Vem comigoo!
O enunciado aqui nos deu uma função e pede para encontrarmos o limites quando e depois vamos determinar o gráfico da função também a partir das interseções com o eixo, olha só como faremos isso!
Primeiro, calcularemos as interseções com os eixos.
As interseções no eixo podem ser calculadas substituindo por , ou seja, , e nesse caso.
As interseções no eixo são encontradas pelas raízes da equação, ou seja,
para isso utilizamos o princípio da multiplicação por , daí, as raízes são:
.
Passo 2
Podemos determinar o sinal de cada fator dependendo se o expoente é ímpar ou par. Se o expoente for par, então o resultado é sempre positivo. Caso contrário, você também deve observar o sinal à frente de cada fator e levar em consideração se o valor de se aproxima de ou .
Agora calcularemos os limites
E
Calculando o primeiro limite
Passo 3
E agora o segundo, analogamente ao primeiro
Note que
Passo 4
Agora, podemos esboçar o gráfico com as informações que de limite e interseção que já temos!
A função intersecta o eixo em e o eixo , e .
A função sobre para quando vai para e desce para quando vai para .
E com o auxilio do GeoGebra, chegamos ao seguinte gráfico!!
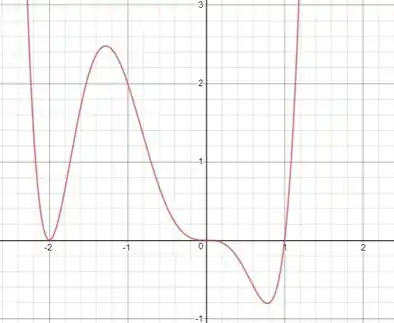
Resposta
