Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.6 - Ex. 53

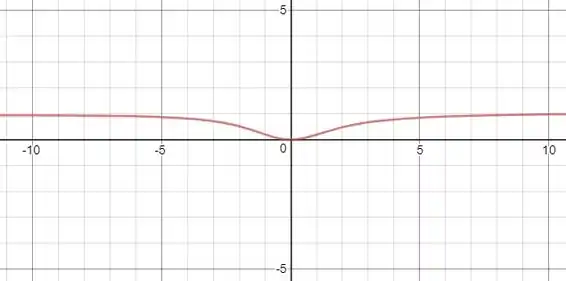
Estime a assíntota horizontal da função

f x = 3 x 3 + 500 x 2 x 3 + 500 x 2 + 100 x + 2000

através do gráfico de f para - 10 ≤ x ≤ 10 . A seguir, determine a equação da assíntota calculando o limite. Como você explica a discrepância?

Passo 1

Olá, meu nobre amigo. Yuri aqui e estarei te ajudando a resolver essa atividade.

Iremos aqui determinar a assíntota horizontal da função dada a partir do seu limite e de seu gráfico.

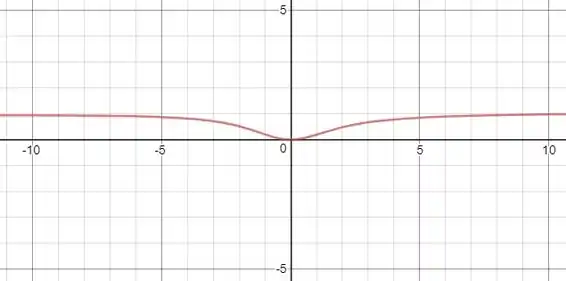
Plotando o gráfico com o auxilio do GeoGebra:

Passo 2

Portanto, ao analisar o gráfico para o intervalo em questão temos que a assíntota horizontal horizontal vale y = 1

Agora, calcularemos a assíntota horizontal, para isso, aplicamos calculamos o limite em que x → ± ∞

lim x → ± ∞ ⁡ 3 x 3 + 500 x 2 x 3 + 500 x 2 + 100 x + 2000

Dividindo o numerador e o denominador por x 3 :

= lim x → ± ∞ ⁡ 3 + 500 x 1 + 500 x + 100 x 2 + 2000 x 3

= 3 + 0 1 + 0 + 0 + 0

lim x → ± ∞ ⁡ 3 x 3 + 500 x 2 x 3 + 500 x 2 + 100 x + 2000 = 3

Passo 3

A discrepância é explicada pois a função cresce muito lentamente, então, para um intervalo pequeno, não é possível observar todo o crescimento da função. Ela possui coeficientes da ordem de milhares (como por exemplo o 2000 presente no polinômio do denominador), então para um intervalo de dezenas o crescimento não é tão acentuado.

Resposta

y = 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

8. Esboce o gráfico de um exemplo de uma função f que satisfaça a todas as condições dadas lim x → ∞ ⁡ f x = 3 ,lim x → 2 - ⁡ f x = ∞ ,lim x → 2 + ⁡ f x = - ∞ , f é ímpar
7. Esboce o gráfico de um exemplo de uma função f que satisfaça a todas as condições dadas lim x → 2 ⁡ f x = - ∞lim x → ∞ ⁡ f x = ∞lim x → - ∞ ⁡ f x = 0 lim x → 0 + ⁡ f x = ∞ lim x → 0 - ⁡ f x = - ∞
22. Encontre o limite ou demonstre que não existe. lim x → ∞ ⁡ x 2 x 4 + 1
Encontre o limite ou demonstra que não existe. lim t → ∞ ⁡ t - t t 2 t 3 / 2 + 3 t - 5
6. Esboce o gráfico de um exemplo de uma função f que satisfaça a todas as condições dadas lim x → 2 ⁡ f x = ∞ lim x → - 2 + ⁡ f x = ∞lim x → - 2 - ⁡ f x = - ∞ lim x → - ∞ ⁡ f x = 0 lim x → ∞ ⁡ f x =