Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.6 - Ex. 63
Encontre os limites quando . Use essa informação, bem como as interseções com os eixos, para fazer um esboço do gráfico.
Passo 1
Falaaa... tudo bem?? Nessa questão foi dada a função:
E é pedido pra calcular os limites quando tende para mais ou menos infinito.
Também é pedido pra encontrar as interseções da função com os eixos e .
Lembrando que a interseção no eixo é quando é igual a zero e a interseção com o eixo é quando é igual a zero.
Com essas informações vamos esboçar o gráfico da função.
Passo 2
Primeiro, calcularemos as interseções com os eixos. As interseções no eixo podem ser calculadas substituindo por 0, ou seja, , e nesse caso:
As interseções no eixo são encontradas pelas raízes da equação, ou seja, , para isso utilizamos o princípio da multiplicação por 0, daí, as raízes são .
Passo 3
Agora calcularemos os limites,
Calculando o primeiro limite,
Calculando o segundo limite, analogamente ao primeiro,
Não se esqueça dos sinais dentro da expressão algébrica, eles são muito importantes.
Passo 4
Agora vamos plotar os pontos de interseção que achamos nos passos anteriores:
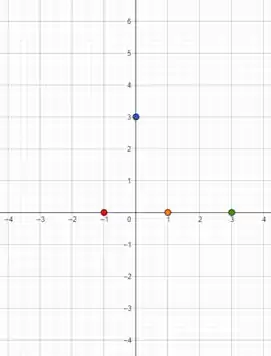
Temos a interseção com o eixo , o ponto azul. Jás os pontos vermelho, laranja e verde são interseção com o eixo .
Também calculamos o limite de quando tende a , que dá . Isso nos dá ideia de que ela vem descendo lááá de cima pelo lado esquerdo.
Já o limite de quando tende a dá . Isso nos dá ideia de que ele continua descendo conforme vai andando pra direita:
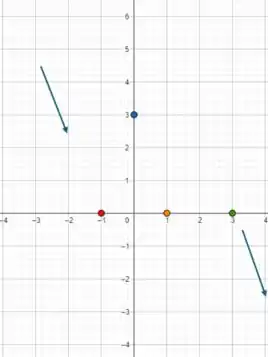
Agora, podemos esboçar o gráfico:
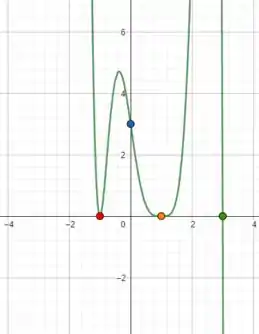
Resposta
Interseção com o eixo :
Interseção com o eixo : , e