Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.6 - Ex. 54
(a)Trace o gráfico da função
Quantas assíntotas verticais e horizontais você observa? Use o gráfico para estimar os valores dos limites
(b)Calculando valores de dê estimativas numéricas dos limites na parte (a)
(c)Calcule os valores exatos dos limites na parte (a). Você obtém os mesmos valores ou valores diferentes para esses limites?
Passo 1
Olá, meu amigo. Yuri aqui e estarei te ajudando a resolver essa atividade.
Inicialmente queremos aqui encontrarmos, a partir do gráfico da função, suas assíntotas verticais e horizontais. A questão nos pede para que façamos isso utilizando o gráfico gerado da função.
- Uma assíntota vertical ocorre quando a função se aproxima de um valor vertical específico à medida que a variável independente se aproxima de um determinado valor;
- As assíntotas verticais podem ocorrer devido a valores que fazem com que a função se torne indefinida, como divisões por zero ou raízes de denominadores polinomiais;
- Uma assíntota horizontal ocorre quando a função se aproxima de um valor horizontal específico à medida que a variável independente se aproxima de ou de ;
- Uma função pode ter uma assíntota horizontal em se a função se aproxima de à medida que se aproxima de
Para encontramos estimativas sobre os valores dos limites por meio de , iremos montar uma tabela, onde colocaremos valores cada vez maiores positivos e negativos, e assim iremos notar para qual valor a nossa função se encaminha.
Passo 2
(a) Plotando o gráfico a partir do GeoGebra, temos:
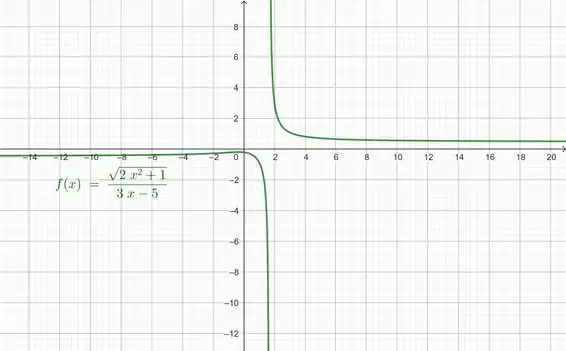
Podemos observar que há duas assíntotas horizontais e uma assíntota vertical.
Temos a vertical e as horizontais em .
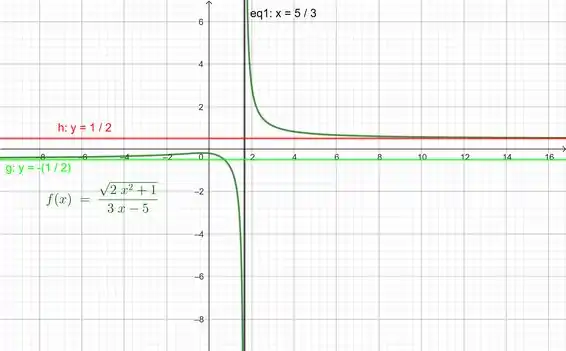
E calculando os limites pelo gráfico, temos
Passo 3
(b) Criaremos uma tabela de confrontando , com valores tendendo a
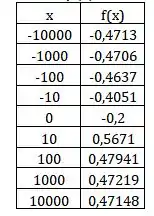
Logo,
Passo 4
(c) Cálculo do limite exato da parte (a)
Dividindo ambos os termos por para que possamos futuramente zerar termos por meio do limite ao infinito:
Colocando o dentro da raiz:
Agora calculando o limite de fato:
Realizando novamente a divisão:
Colocando dentro da raiz:
Agora há uma parte complicada quando você move para o interior. Um sinal negativo deve ser colocado do lado de fora para preservar o sinal original de toda a expressão. Veja dessa forma, , então ambos os que você está multiplicando são negativos, o que se cancelaria mutuamente, o que é o que você quer porque você só multiplica por "1" para não alterar o valor da expressão. Se você move um deles para dentro da raiz quadrada, você precisa deixar um negativo do lado de fora para preservar esse equilíbrio. Você pode verificar inserindo um número negativo para nas versões original e após essa manipulação, que ela está correta.
Agora calculando o limite individualmente:
Resposta
- Podemos observar que há duas assíntotas horizontais e uma assíntota vertical. Temos a vertical e as horizontais em