Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 3.Exercícios Práticos - Ex. 153a
Encontre as linearizações de
a.
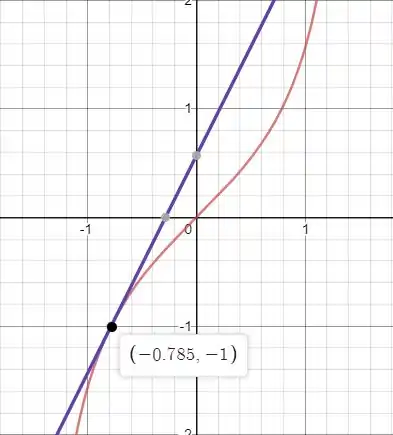
Trace as curvas e as linearizações em um único gráfico.
Passo 1
Da definição de linearização, temos que se a função é derivável para um valor dado, então:
Para este caso, temos que:
Passo 2
Portanto, para encontrar a linearização devemos determinar o valor da função dada e da sua derivada no ponto especificado. Logo:
Passo 3
Substituindo os valores do ponto dado, da função e de sua derivada na equação da linearização conseguimos obter o que foi pedido:
Resposta
Exercícios de Livros Relacionados
Tanto x quanto y denotam funções de t que estão relacionadas pela equação dada. Use essa equação e a informação sobre a derivada para encontrar a derivada especificada.Equação: y=3 x+5 .(a) Dado que d
Uma pedra jogada em um lago produz uma onda circular, cujo raio cresce a uma taxa constante de 1m / s . Com que rapidez estará variando a área englobada pela onda crescente ao final de 10 segundos?
Um balão esférico é esvaziado de tal forma que seu raio decresce a uma taxa constante de 15c m / m i n . Com que taxa o ar estará sendo removido quando o raio for de 9c m ?
Um balão esférico é inflado de tal forma que seu volume cresce a uma taxa de 3c m 3 / m i n . Com que rapidez o diâmetro do balão estará crescendo quando o raio for de 1c m ?
Seja A a área de um quadrado cujos lados têm comprimento x e suponha que x varie com o tempo t . (a) Faça uma figura do quadrado com os dados A e x colocados apropriadamente. (b) Escreva uma equação q