Enunciado
Álgebra Linear e Geometria Analítica - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 13.2 - Ex. 32
Encontre o módulo da força resultante e o ângulo que ela faz com o eixo positivo.
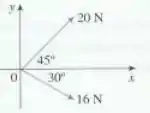
28. 
Passo 1
Para encontrar a força resultante, nós precisaremos decompor os dois vetores, somar suas componentes e então calcular o módulo do vetor resultante.
Vamos chamar de o vetor com módulo igual . Decompondo ele temos:
Substituindo os valores:
Agora vamos decompor o outro vetor, .
Repare que a componente do vetor é negativa, pois está na parte negativa do eixo .
Para encontrarmos o vetor resultante , basta somarmos as componentes de e , assim:
Show! Agora só precisamos encontrar o módulo desse vetor!
Passo 2
Agora que já temos o módulo do vetor resultante, queremos encontrar também qual o ângulo que ele faz com o eixo , esse ângulo pode ser dado por
Resposta
28.
Exercícios de Livros Relacionados
Seja B = i → ,j → ,k → a base ortonormal obtida da base E = e → 1 ,e → 2 ,e → 3 pelo Processo de Ortonormalização de Gram-Schmidt. A matriz de mudança de E para B tem um aspecto muit especial. Descrev
Prove que:a) p r o j u →v → = v → se, e somente se, u → ,v → é LD;b) p r o j u →v → = u → se, e somente se, ( v → - u → ) ⊥ u → ;c) se A , B e C são pontos distintos e A C → = p r o j A C →A B → , ent
Prove que:a) u → ⋅ v → ≤ u → v → ;b) vale a igualdade em (a) se, e somente se, u → ,v → é LD;c) u → + v → ≤ u → + v → ;d) | u → - v → | ≤ u → - v → e) uma condição necessária e suficiente para que val
Na Figura 9-12 está representado um cubo de aresta unitária. Sejam e → 1 = D H → , e → 2 = D C → , e → 3 = D A → , u → = C D → + C B → , v → = D C → + C B → e w → = G C → .a) Explique por que E = e →
Prove que:A mediana e a altura relativas à base de um triângulo isósceles coincidem, e estão contidas na bissetriz do ângulo do vértice;Um triângulo é isósceles se, e somente se, ele tem dois ângulos