Enunciado

Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 9.Exercício - Ex. 44

Prove que:

A mediana e a altura relativas à base de um triângulo isósceles coincidem, e estão contidas na bissetriz do ângulo do vértice;

Um triângulo é isósceles se, e somente se, ele tem dois ângulos internos congruentes.

Passo 1

Vou te dar uma notícia boa: esse exercício conseguimos resolver ele todo numa jogada só!

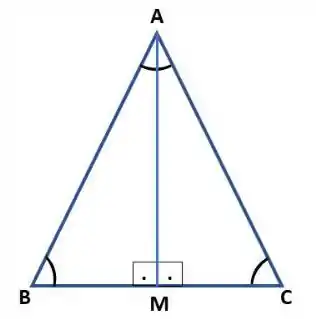
Para provar essas duas propriedades, vamos utilizar um triângulo isósceles ABC. Se traçarmos a bissetriz do ângulo no vértice, formamos os triângulos ABM e ACM, igual o da figura abaixo.

Passo 2

Se voce reparar, o lado é comum aos dois triângulos e a bissetriz dividiu o ângulo em dois ângulos de mesma medida. Beleza?!

Além disso, os lados e são congruentes, pois tem os lados iguais do triângulo isósceles . Show de bola?!

Então, temos o caso de congruência de triângulos LAL (lado, ângulo, lado)!!

Concluímos então que os ângulos , da base do triângulo, possuem a mesma medida. Show!? Então a letra (b) já ta provada!

Tá conseguindo acompanhar o raciocínio?? Então vamos continuar!

Passo 3

Podemos concluir também que, como os triângulos e são congruentes, as medidas de e são iguais.

Assim, é a mediana relativa à base. Além disso, também é a altura relativa à base, pois forma com a base dois ângulos iguais a 90º. Logo, mostramos a letra (a) e a letra (b)!!