Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 9.Exercício - Ex. 68

Na Figura 9-12 está representado um cubo de aresta unitária. Sejam e → 1 = D H → , e → 2 = D C → , e → 3 = D A → , u → = C D → + C B → , v → = D C → + C B → e w → = G C → .

a) Explique por que E = e → 1 , e → 2 ,   e → 3 é uma base ortonormal.

b) Calcule as coordenadas de u → , v → e w → na base E , e obtenha u → e v → .

c) Sejam f → 1 e f → 2 , respectivamente, os versores de u → e v → . Prove que F = f → 1 ,   f → 2 ,   w → é uma base ortonormal.

d) Obtenha a matriz de mudança de E para F , bem como a matriz de mudança de F para E .

e) Calcule as coordenadas de   H B → na base E e na base F .

Passo 1

Para explicar porque E é uma base ortonormal, vamos olhar para o cubo:

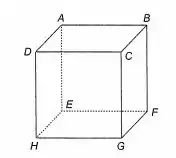
Note que todos os vetores de E são arestas do cubo que são ortogonais entre si. Além disso, como todos os lados do cubo medem 1 , eles são unitários. Sendo assim, E é uma base ortonormal.

Passo 2

O vetor u → pode ser escrito como:

u → = C D → + C B → = - D C → + C B →

Como   C B → = D A → :

u → = - D C → + D A → = - e → 2 + e → 3 = 0 ,   - 1 ,   1 E

Já v → :

v → = D C → + C B → = D C → + D A → = e → 2 + e → 3 = 0 ,   1 ,   1 E

Por fim,

w → = G C → = H D → = - D H → = - e → 1 = - 1 ,   0 ,   0 E

Passo 3

Agora vamos analisar primeiro a base A = u → ,   v → ,   w → . Note que

u → ⋅ v → = 0 - 1 + 1 = 0

u → ⋅ w → = 0 + 0 + 0 = 0

v → ⋅ w → = 0 + 0 + 0 = 0

Assim, A é uma base ortogonal, mas não ortonormal pois

u → = v → = 2

Mas como f → 1 e f → 2 são os versores de u → e v → :

f → 1 = 0 , - 1 2 , 1 2 E

f → 2 = 0 , 1 2 , 1 2 E

Assim, a base F = f → 1 ,   f → 2 ,   w → é ortonormal, pois w → = f → 1 = f → 2 = 1 .

Passo 4

Para construir a matriz de mudança de base de E para F , basta usar as coordenadas dos vetores de F na base E :

M E F = 0 0 - 1 - 1 2 1 2 0 1 2 1 2 0

Agora, para achar M F E basta inverter M E F . Como as bases são ortonormais, a inversa é igual a transposta:

M F E = M E F - 1 = M E F T

Assim,

M F E = 0 - 1 2 1 2 0 1 2 1 2 - 1 0 0

Passo 5

Vamos escrever primeiro   H B → na base E :

H B → = H D → + D A → + A B → = - D H → + D A → + D C → = - e → 1 + e → 2 + e → 3 = - 1 ,   1 ,   1 E

Usando a matriz de mudança de base:

x y z F = M F E   - 1 1 1 E = 0 - 1 2 1 2 0 1 2 1 2 - 1 0 0   - 1 1 1 E

Assim,

x y z F = 0 2 2 1

Portanto,

H B → = - 1 ,   1 ,   1 E = 0 , 2 2 ,   1 F

Resposta

u → = 0 ,   - 1 ,   1 E ,               v → = 0 ,   1 ,   1 E ,               w → = - 1 ,   0 ,   0 E

M E F = 0 0 - 1 - 1 2 1 2 0 1 2 1 2 0

M F E = 0 - 1 2 1 2 0 1 2 1 2 - 1 0 0

H B → = - 1 ,   1 ,   1 E = 0 , 2 2 ,   1 F

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Os ângulos diretores de um vetor podem ser 45 ° , 60 ° e 90 ° ? Justificar.
Determine o vetor v → , colinear ao vetor u → = - 4 ,2 ,6 , tal que v → ∙ w → = - 12 sendo w → = - 1 ,4 ,2 .
Os lados de um triângulo retângulo A B C (reto em A ) medem 5, 12 e 13. Calcular A B → ∙ A C → + B A → ∙ B C → + C A → ∙ C B →
Calcular n para que seja de 30 ° o ângulo entre os vetores u → = ( 1 ,n ,2 ) e j → .
Determinar o vetor v → , ortogonal ao eixo O z , que satisfaz as condições v → ∙ v → 1 = 10 e v → ∙ v → 2 = - 5 , sendo v → 1 = 2 ,3 ,- 1 e v → 2 = 1 ,- 1 ,2 .