Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 6.1 - Ex. 51
Encontre o número tal que a reta divida a região delimitada pelas curvas e em duas regiões com área igual.
Passo 1
Opa, bora resolver esse problema! Temos as curvas:
e
E o enunciado pede pra a gente encontrar uma reta que divide a região definida por e em duas áreas iguais:
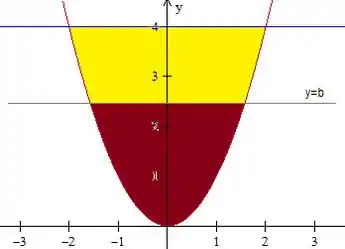
Para descobrir as áreas, vamos integrar em relação à , pois dessa forma ficará mais simples escrevermos as integrais.
Passo 2
Vamos escrever a função tendo como variável :
Teremos agora um gráfico invertido:
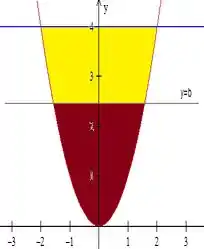
Passo 3
Vamos escrever as áreas como integrais, lembrando que a área marrom () é igual a área amarela ():
Aplicando os limites de integração:
Chegamos em:
Prontinho!
Resposta
Exercícios de Livros Relacionados
7-18 Esboce a região englobada pelas curvas e encontra a área7. y = x 2 , y = x , x = 1 4 , x = 1
19-26.19. Use um recurso gráfico computacional, quando necessário, para encontra a região englobada pelas curvas.19. y = x 3 - 4 x 2 + 3 x
7-18 Esboce a região englobada pelas curvas e encontra a área11. x = sin y , x = 0 , y = π / 4 , y = 3 π / 4
19-26.Use um recurso gráfico computacional, quando necessário, para encontra a região englobada pelas curvas.22. y = x 3 - 4 x ,y = 0
7-18 Esboce a região englobada pelas curvas e encontra a área13. y = e x , y = e 2 x , x = 0 , x = ln 2 .