Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 4.1 - Ex. 37
Encontre os números críticos da função.
Passo 1
Oi, oi meus caros, como vocês estão?
Nessa questão temos a seguinte função:
E queremos encontrar os números críticos da função.
Vamos começar entendendo o que vem a ser esse tal de “número crítico”.
Um número crítico é nada mais, nada menos que um número onde sua derivada é igual a zero
ou não existe
Além disso, aqui temos uma função que é dada em módulo, por isso, vale lembrar que a função módulo nada mais é que uma função dada em partes:
Certinho??
Passo 2
Desse modo, é preciso analisar o módulo.
Para
temos:
Resolvendo a inequação, temos:
Passo 3
Derivando , vamos derivar ela em cada intervalo:
Para , temos:
Essa derivada nunca será zero.
Derivando agora no outro intervalo:
Para , temos:
Essa derivada também nunca será zero.
Portanto, não há valores para os quais que façam com que a derivada seja zero .
Passo 4
No entanto, também é definido como número crítico, um ponto onde a derivada não exista.
Se olharmos para o comportamento da derivada dessa função, vemos que:
Se você apenas derivar a função módulo, vai acreditar que para .
No entanto, a derivada precisa ser uma função contínua no ponto para existir naquele ponto.
E ela não é contínua em . Para valores maiores que esse, a derivada vale e para valores menores que esse a derivada vale .
Portanto, exatamente nesse ponto, a derivada não existe.
A forma correta de definir a derivada dessa função é:
Portanto, é um número crítico da nossa função.
Para te provar isso, vou trazer o gráfico da função:
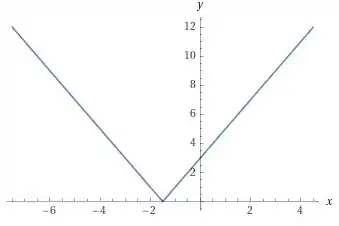
E o gráfico da sua derivada.
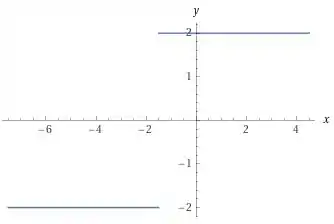
Percebe que exatamente em , a função tem um bico.
Não tem como definir qual a derivada nesse ponto, pois a função tem um comportamento que se altera drasticamente nesse ponto.