Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 4.1 - Ex. 6
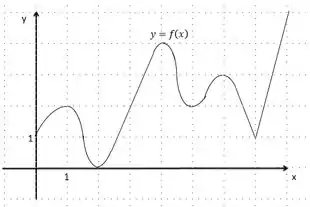
Use o gráfico para estabelecer os valores de máximo e mínimo locais e absolutos da função.
Passo 1
E aí, beleza? Bora entender essa questão juntos 😊?
Apenas utilizando o gráfico da função dado, a questão quer que a gente encontre os pontos em que a assume:
- Valores de máximo e mínimo globais.
- Valores de máximo e mínimo locais.
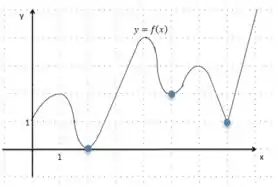
O nosso gráfico é:
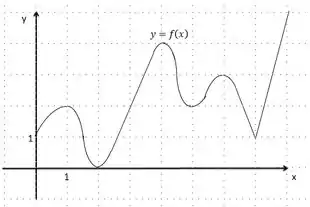
Mas, para fazer isso, precisamos saber o que são tais valores, certo?
De uma maneira BEEEEEEEEM simples e intuitiva, dizemos que a principal diferença entre os valores locais e globais é que os valores locais são os picos e vales dentro de uma área específica, enquanto os valores globais são os pontos mais altos e mais baixos em todo o gráfico da função.
Colocando em termos um pouco mais teóricos:
- O máximo local é um valor para qualquer bem próximo de
- Da mesma forma, o mínimo local é um valor para qualquer bem próximo de .
Enquanto:
- o máximo absoluto é o maior valor que a função atinge em todo o seu domínio. Ou seja, para qualquer no domínio.
- Da mesma forma, o mínimo absoluto é o menor valor que a função atinge em todo o seu domínio. Ou seja, para qualquer no domínio.
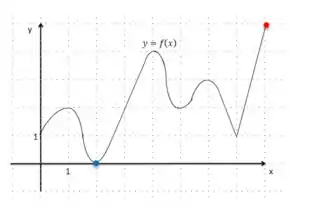
- O ponto vermelho é o ponto mais alto no gráfico de . Dessa forma, o valor de máximo absoluto é quando e ocorre quando .
- O ponto azul é o ponto mais baixo do gráfico. Dessa forma, o valor de mínimo absoluto é quando e ocorre quando .
- Os pontos vermelhos e são picos do gráfico. Dessa forma, os valores de máximo locais são:
- e ocorre quando .
- e ocorre quando .
- e ocorre quando .
- Os pontos azuis e são vales do gráfico. Dessa forma, os valores de mínimo locais são:
- e ocorre quando .
- e ocorre quando .
- e ocorre quando .
Já temos tudo o que precisamos para analisar o gráfico e obter os valores pedidos. Bora lá 😊!
Passo 2
Começamos encontrando os máximos e mínimos absolutos!
Máximo absoluto:
🧐 Olhando para o gráfico da função, qual é o ponto do seu gráfico que está mais no alto? Matematicamente você tem que pensar o seguinte: qual é o ponto no gráfico da função que possui o MAIOR valor em sua ordenada ?
Mínimo absoluto:
🧐 De novo, olhando para o gráfico da função, qual é o ponto do seu gráfico que está mais embaixo? Matematicamente: qual é o ponto no gráfico da função que possui o MENOR valor em sua ordenada ?
Passo 3
Agora, vamos encontrar os máximos e mínimos locais!
Máximos locais:
🧐 Olhando para o gráfico, quais são os pontos que são picos de uma determinada região? Matematicamente: quais são os pontos no gráfico da função que, ao seu redor, nenhum outro ponto tem a ordenada MAIOR do que a sua?
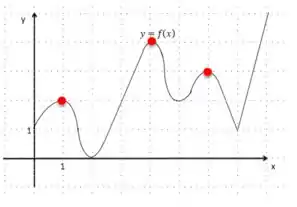
Mínimos locais:
🧐 Olhando para o gráfico, quais são os pontos que são vales de uma determinada região? Matematicamente: quais são os pontos no gráfico da função que, ao seu redor, nenhum outro ponto tem a ordenada MENOR do que a sua?
Passo 2
Já respondemos à questão, mas você notou que o ponto de mínimo absoluto é também ponto de mínimo local? Enquanto o ponto de máximo global não é mínimo absoluto?
Isso ocorre porque o ponto de máximo absoluto está no extremo do intervalo (domínio da função) e, com isso, ele não pode ser um extremo local, já que não temos informações sobre o que ocorre na vizinhança dele.
Resposta
O valor máximo absoluto é e ocorre quando .
O valor mínimo absoluto é e ocorre quando .
Os valores de máximo locais são:
Os valores de mínimo locais são: