Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 11.12 - Ex. 8
Encontre o polinômio de Taylor da função em . Trace e na mesma tela.
Passo 1
Neste caso, consegue ver que as derivadas vão ficar um pouco complicadas com o aumento de ? Então não vamos buscar um padrão para a série, vamos só calcular os termos com , que vai nos dar o direto.
Então derivando e substituindo que é o nosso centro
Passo 2
Como temos as derivadas no centro das três primeiras derivadas, respeitando a fórmula da série de Taylor
Para calcularmos precisamos apenas do grau 3 e inferiores, então temos que
Passo 3
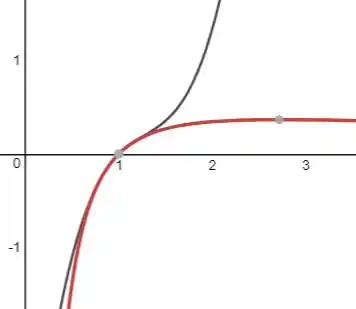
Traçando a função e no plano
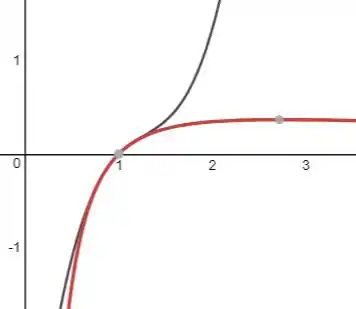
De vermelho temos a função e em cinza .
Resposta
Exercícios de Livros Relacionados
Use a definição da série de Taylor para encontrar os quatro primeiros termos não nulos da série para f ( x ) centrada no valor dado de a . f x = sen x , a = π 6
Encontre a série de Maclaurin para f ( x ) usando a definição da série de Maclaurin. [Assuma que f possui uma expansão em série de potências. Não mostre que R n x → 0 . ] Encontre também o raio de con
Encontre a série de Maclaurin para f ( x ) usando a definição da série de Maclaurin. [Assuma que f possui uma expansão em série de potências. Não mostre que R n x → 0 . ] Encontre também o raio de con
Encontre a série de Maclaurin para f ( x ) usando a definição da série de Maclaurin. [Assuma que f possui uma expansão em série de potências. Não mostre que R n x → 0 . ] Encontre também o raio de con
Use as séries de Maclaurin da Tabela 1 para obter a série de Maclaurin para a função dada. f x = arctg x 2